Demonstration of Well Class

Notebook to demonstrate using the Well Class to estimate drawdown or stream depletion using the solutions available in the python module.

import sys

sys.path.insert(1, "../../")
import pycap
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

Example Depletion

The Well class will estimate depletions for streams. The stream distances and streambed conductances, if needed, are passed through dictionaries keyed by a stream name or ID. In this notebook a table of values will be made manually from Table 2 from Reeves, H.W., Hamilton, D.A., Seelbach, P.W., and Asher, A.J., 2009, Ground-water-withdrawal component of the Michigan water-withdrawal screening tool: U.S. Geological Survey Scientific Investigations Report 2009–5003, 36 p. [https://pubs.usgs.gov/sir/2009/5003/]

pro tip: notice that the distance increases with increasing ID number. Useful for relative reference below.

stream_table = pd.DataFrame(
    (
        {"id": 8, "distance": 14802},
        {"id": 9, "distance": 12609.2},
        {"id": 11, "distance": 15750.5},
        {"id": 27, "distance": 22567.6},
        {"id": 9741, "distance": 27565.2},
        {"id": 10532, "distance": 33059.5},
        {"id": 11967, "distance": 14846.3},
        {"id": 12515, "distance": 17042.55},
        {"id": 12573, "distance": 11959.5},
        {"id": 12941, "distance": 19070.8},
        {"id": 13925, "distance": 10028.9},
    )
)

Compute apportionment

The example in the report uses inverse-distance weighting apportionment. Other apportionment approaches that may be used as a simple way to extend the analytical solution are discussed by Zipper and others (2019). [https://agupubs.onlinelibrary.wiley.com/doi/10.1029/2018WR024403]

invers = np.array([1 / x for x in stream_table["distance"]])
stream_table["apportionment"] = (1.0 / stream_table["distance"]) / np.sum(invers)

set aquifer properties and streambed conductances

T = 7211.0  # ft^2/day
S = 0.01
Q = 70  # 70 gpm --> must convert to cubic feet per day
pumpdays = int(5.0 * 365)
stream_table["conductance"] = 7.11855  # example uses constant streambed_conductance

call a utility to convert Q to a series with appropriate formatting

The Well Class works with a Pandas series of pumping rates, it may be easily constructed with the pycap-dss Q2ts function. The index of the series is pumping days. We also need to convert from pumping in GPM to cubic feet per day so that units are consistent.

Q = pycap.Q2ts(pumpdays, 5, Q) * pycap.GPM2CFD

Q

1       13475.935829
2       13475.935829
3       13475.935829
4       13475.935829
5       13475.935829
            ...
1821    13475.935829
1822    13475.935829
1823    13475.935829
1824    13475.935829
1825    13475.935829
Length: 1825, dtype: float64

stream_table.head()

	id	distance	apportionment	conductance
0	8	14802.0	0.098916	7.11855
1	9	12609.2	0.116118	7.11855
2	11	15750.5	0.092959	7.11855
3	27	22567.6	0.064878	7.11855
4	9741	27565.2	0.053116	7.11855

make dictionaries from the distances, apportionment, and conductance values

distances = dict(zip(stream_table.id.values, stream_table.distance.values))

apportion = dict(zip(stream_table.id.values, stream_table.apportionment.values))

cond = dict(zip(stream_table.id.values, stream_table.conductance.values))

Make a Well object

Depletion and drawdown can be easily returned as attributes of the object. The choice of depletion or drawdown method is made through a parameter passed to the object. In this example the Hunt (1999) depletion method is used to compute stream depletion for the dictionary of streams at the given distances with the inverse-distance apportionment. We also can compute drawdown at a dictionary of locations. If drawdown_dist is not passed to the object, then drawdowns will not be computed. Results are returned as arrays that may easily be converted to Pandas dataframes for ease of viewing and plotting.

test_well = pycap.Well(
    T=T,
    S=S,
    Q=Q,
    depletion_years=5,
    depl_method="hunt_99_depletion",
    drawdown_dist={"testlocation0": 50.0},  # default method is Theis
    streambed_conductance=cond,
    stream_dist=distances,
    stream_apportionment=apportion,
)

drawdown = pd.DataFrame(test_well.drawdown)

look at drawdown, only one distance was specified. The timeseries is returned however.

drawdown.head()

	testlocation0
0	0.000000
1	0.962843
2	1.065859
3	1.126136
4	1.168908

Depletion

The object gives the daily time series according to the pumping schedule. We can pull out the 5-year depletion to note that the final results match Table 2. Note that we need to convert to GPM to compare results to Table 2

stream_depl = pd.DataFrame(test_well.depletion)

stream_depl = stream_depl * pycap.CFD2GPM
# pull out row for days = 1824 and transpose matrix for ease of comparison to Table 2
five_year = pd.DataFrame(stream_depl.loc[1824].T)
five_year.rename(columns={1824: "Depletion"}, inplace=True)
five_year

	Depletion
8	5.144899
9	6.303955
11	4.744429
27	2.869554
9741	2.098081
10532	1.532334
11967	5.125042
12515	4.271490
12573	6.729668
12941	3.660252
13925	8.322122

What about plotting?

fig, ax = plt.subplots()
drawdown.plot(ax=ax)
ax.set_xlabel("pumping in days")
ax.set_ylabel("drawdown in feet")

Text(0, 0.5, 'drawdown in feet')

fig, ax = plt.subplots()
stream_depl.plot(ax=ax)
ax.set_xlabel("pumping in days")
ax.set_ylabel("depletion in GPM")
ax.legend(
    title="Explanation",
    bbox_to_anchor=(0, 0.9, 1, 0.9),
    bbox_transform=fig.transFigure,
    ncols=5,
    mode="expand",
    loc="lower left",
)

<matplotlib.legend.Legend at 0x161b83d90>

Change depletion method

Several depletion methods are available (see the solutions demonstation notebook for more information). The choice of depletion method is passed to the object as a parameter. Some solutions require additional parameters which need to be passed as named variables.

pycap.ALL_DEPL_METHODS

{'glover_depletion': <function pycap.solutions.glover_depletion(T, S, time, dist, Q, **kwargs)>,
 'walton_depletion': <function pycap.solutions.walton_depletion(T, S, time, dist, Q, **kwargs)>,
 'hunt_99_depletion': <function pycap.solutions.hunt_99_depletion(T, S, time, dist, Q, streambed_conductance=None, **kwargs)>,
 'hunt_03_depletion': <function pycap.solutions.hunt_03_depletion(T, S, time, dist, Q, Bprime=None, Bdouble=None, aquitard_K=None, sigma=None, width=None, streambed_conductance=None, **kwargs)>,
 'ward_lough_depletion': <function pycap.solutions.ward_lough_depletion(T1, S1, t, dist, Q, T2=None, S2=None, width=None, streambed_thick=None, streambed_K=None, aquitard_thick=None, aquitard_K=None, NSteh1=2, **kwargs)>}

# for example the Glover and Balmer solution for a stream assuming no streambed resistance. Note that
# the streambed_conductance parameter can be dropped from the call.
test_glover = pycap.Well(
    T=T,
    S=S,
    Q=Q,
    depletion_years=5,
    depl_method="glover_depletion",
    drawdown_dist={"testlocation0": 50.0},  # default method is Theis
    stream_dist=distances,
    stream_apportionment=apportion,
)

glover_depl = pd.DataFrame(test_glover.depletion)
glover_depl = glover_depl * pycap.CFD2GPM

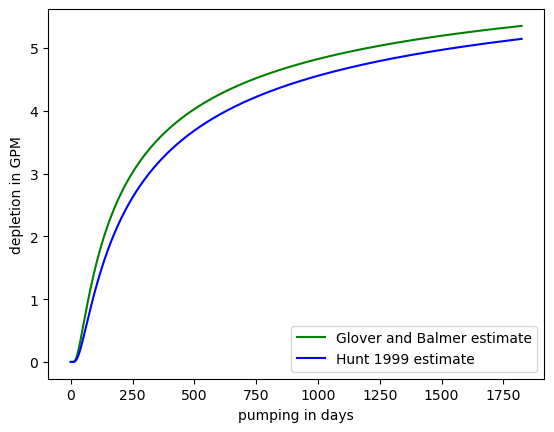
# plot the two solutions to compare depletion estimates

fig, ax = plt.subplots()
ax.plot(
    glover_depl.index.values,
    glover_depl[8].values,
    "g-",
    label="Glover and Balmer estimate",
)
ax.plot(
    stream_depl.index.values, stream_depl[8].values, "b-", label="Hunt 1999 estimate"
)
ax.set_xlabel("pumping in days")
ax.set_ylabel("depletion in GPM")
ax.legend(loc="lower right")

<matplotlib.legend.Legend at 0x161bd94d0>

Intermittent Pumping

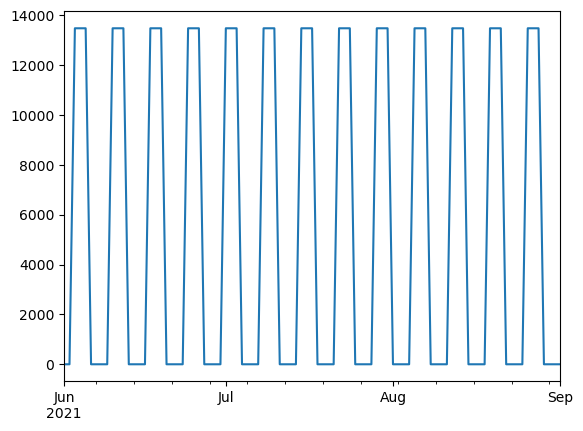
The Well Class accepts Q as a series of daily pumping rates and will use superposition to produce a timeseries of drawdown or depletion. The Q2ts helper function is one way to generate an input series, but the user can make an arbitrary series.

Set up a series pumping 3 days a week during June, July, and August

Q_series = pd.Series(
    index=pd.period_range(start="2020-10-01", end="2025-09-30", freq="D")
)

for d in Q_series.index.values:
    Q_series[d] = 0.0
    if d.month in range(6, 9):
        if d.dayofweek in range(3, 6):
            Q_series[d] = 70 * pycap.GPM2CFD

fig, ax = plt.subplots()
Q_series.plot(ax=ax)
ax.set_xlim("2021-06-01", "2021-09-01")

(18779.0, 18871.0)

Well Class expects series index to be integer days

Q_days = pd.Series(Q_series.values, index=range(1, len(Q_series) + 1))

Q_days

1       0.0
2       0.0
3       0.0
4       0.0
5       0.0
       ...
1822    0.0
1823    0.0
1824    0.0
1825    0.0
1826    0.0
Length: 1826, dtype: float64

test_intermittent = pycap.Well(
    T=T,
    S=S,
    Q=Q_days,
    depletion_years=5,
    depl_method="hunt_99_depletion",
    drawdown_dist={"testlocation0": 50.0},  # default method is Theis
    streambed_conductance=cond,
    stream_dist=distances,
    stream_apportionment=apportion,
)

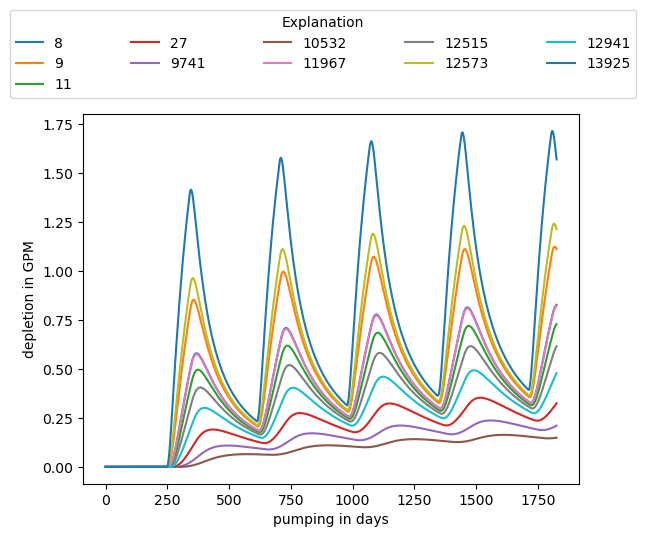
intermittent_depl = pd.DataFrame(test_intermittent.depletion) * pycap.CFD2GPM

fig, ax = plt.subplots()
intermittent_depl.plot(ax=ax)
ax.set_xlabel("pumping in days")
ax.set_ylabel("depletion in GPM")
ax.legend(
    title="Explanation",
    bbox_to_anchor=(0, 0.9, 1, 0.9),
    bbox_transform=fig.transFigure,
    ncols=5,
    mode="expand",
    loc="lower left",
)

<matplotlib.legend.Legend at 0x1619e1350>

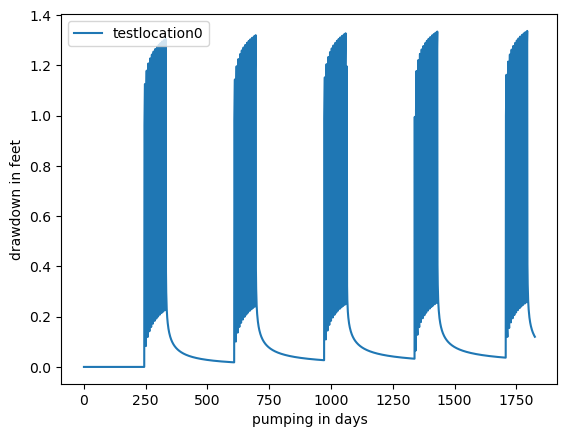
Recall from above that only a single drawdown location was passed to the Well

intermittent_drawdown = pd.DataFrame(test_intermittent.drawdown)

fig, ax = plt.subplots()
intermittent_drawdown.plot(ax=ax)
ax.set_xlabel("pumping in days")
ax.set_ylabel("drawdown in feet")
ax.legend(loc="upper left")

<matplotlib.legend.Legend at 0x161de9ed0>

Well Class is restricted to Theis drawdown

There are drawdown estimates using the Hunt (1999) and Ward and Lough (2011) solutions; but the Well Class is not currently set up to use these solutions. The user should call the functions directly.

Uncomment the following block and run it to see the error in trying to use other drawdown functions.

# test_intermittent = pycap.Well(T=T,
#                  S=S,
#                  Q=Q_days,
#                  depletion_years=5,
#                  depl_method='hunt_99_depletion',
#                  drawdown_dist={'testlocation0':50.},  #default method is Theis
#                  drawdown_method='hunt_99_drawdown',
#                  streambed_conductance=cond,
#                  stream_dist=distances,
#                  stream_apportionment=apportion)