
Seasonal Analysis in EGRET
Robert M. Hirsch and Laura DeCicco
2019-10-02
Source:vignettes/SeasonalFraction.Rmd
SeasonalFraction.RmdIntroduction
This document describes how to obtain seasonal information from the R package EGRET. For example, we might want to know the fraction of the load that takes place in the winter season (say that is December, January, and February). We can look at the seasonal information for a single year, or averages over several years, or in terms of flow normalized fluxes.
Getting started
First, you need to have installed and loaded the EGRET
package. Then, you’ll need need to create an eList object.
See the EGRET vignette or user guide here for more information on
how to use your own water quality data in EGRET. Once the
eList object has been created, run the
modelEstimation function to create a WRTDS model.
For this post, we will use the Choptank River, measuring Inorganic nitrogen (nitrate and nitrite) as an example.
To start with lets look at the results calculated for complete water years.
water_year <- tableResults(eList)##
## Choptank River
## Inorganic nitrogen (nitrate and nitrite)
## Water Year
##
## Year Discharge Conc FN_Conc Flux FN_Flux
## cms mg/L 10^6 kg/yr
##
## 1980 4.25 0.949 1.003 0.1154 0.106
## 1981 2.22 1.035 0.999 0.0675 0.108
## 1982 3.05 1.036 0.993 0.0985 0.110
## 1983 4.99 1.007 0.993 0.1329 0.112
## 1984 5.72 0.990 1.002 0.1597 0.114
## 1985 1.52 1.057 1.017 0.0489 0.116
## 1986 2.63 1.062 1.038 0.0903 0.119
## 1987 3.37 1.079 1.062 0.1142 0.122
## 1988 1.87 1.120 1.085 0.0660 0.125
## 1989 5.61 1.055 1.105 0.1638 0.127
## 1990 4.01 1.115 1.125 0.1349 0.129
## 1991 2.75 1.172 1.143 0.0980 0.130
## 1992 2.19 1.203 1.159 0.0810 0.132
## 1993 3.73 1.215 1.173 0.1306 0.132
## 1994 5.48 1.144 1.187 0.1634 0.133
## 1995 2.41 1.266 1.201 0.0928 0.134
## 1996 6.24 1.134 1.213 0.1980 0.135
## 1997 5.83 1.180 1.221 0.1884 0.136
## 1998 4.88 1.236 1.229 0.1593 0.137
## 1999 2.90 1.277 1.238 0.0919 0.138
## 2000 4.72 1.213 1.253 0.1627 0.139
## 2001 4.88 1.251 1.268 0.1655 0.140
## 2002 1.24 1.321 1.285 0.0483 0.141
## 2003 8.64 1.140 1.303 0.2664 0.143
## 2004 5.28 1.274 1.321 0.1832 0.144
## 2005 3.81 1.360 1.341 0.1444 0.146
## 2006 3.59 1.382 1.362 0.1409 0.147
## 2007 4.28 1.408 1.382 0.1593 0.149
## 2008 2.56 1.477 1.401 0.1008 0.149
## 2009 3.68 1.409 1.419 0.1328 0.149
## 2010 7.19 1.323 1.438 0.2236 0.149
## 2011 5.24 1.438 1.457 0.1554 0.148
water_year_2010_flux <- water_year$`FN Flux [10^6kg/yr]`[water_year$Year == 2010]Looking at the last column of these results we see that, for example, the flow normalized flux in water year 2010 is estimated to be 0.149 106 kg/year. Now, let’s say we had a particular interest in the winter season which we define here as the months of December, January, and February.
The next step is to establish what season you are interested in
looking at. All functions in EGRET can be done on the
“water year” (Oct-Sept), the calendar year (Jan-Dec), or any set of
sequential months. To define what period of analysis (PA) to use, there
is a function setPA. The setPA function has
two arguments:
-
paStartis the number of the calendar month that is the start of the season.
-
paLongis the length of the season in months (it can be any number from 1 to 12).
For example let’s say we want to consider the winter, defined here as
December through February, the starting month (paStart)
would be 12, and the length (paLong) would be 3:
eList <- setPA(eList, paStart = 12, paLong = 3)Now lets view our results when we are focusing on the winter season.
winter <- tableResults(eList)##
## Choptank River
## Inorganic nitrogen (nitrate and nitrite)
## Season Consisting of Dec Jan Feb
##
## Year Discharge Conc FN_Conc Flux FN_Flux
## cms mg/L 10^6 kg/yr
##
## 1980 4.220 1.10 1.11 0.1403 0.156
## 1981 1.960 1.20 1.13 0.0735 0.161
## 1982 5.057 1.16 1.15 0.1764 0.165
## 1983 3.504 1.21 1.16 0.1310 0.169
## 1984 8.437 1.12 1.18 0.2624 0.173
## 1985 2.249 1.24 1.21 0.0884 0.177
## 1986 5.087 1.25 1.24 0.1902 0.182
## 1987 7.730 1.23 1.27 0.2707 0.187
## 1988 2.590 1.29 1.29 0.1039 0.191
## 1989 3.327 1.36 1.31 0.1400 0.193
## 1990 4.609 1.35 1.33 0.1928 0.195
## 1991 3.883 1.36 1.33 0.1559 0.196
## 1992 2.303 1.40 1.33 0.1015 0.195
## 1993 4.421 1.36 1.32 0.1877 0.194
## 1994 5.849 1.31 1.31 0.2072 0.193
## 1995 3.693 1.37 1.31 0.1543 0.192
## 1996 7.151 1.29 1.31 0.2618 0.193
## 1997 11.786 1.18 1.32 0.3718 0.193
## 1998 9.308 1.27 1.32 0.2979 0.194
## 1999 2.526 1.32 1.33 0.1091 0.196
## 2000 4.785 1.39 1.35 0.1995 0.198
## 2001 5.392 1.39 1.37 0.2194 0.200
## 2002 0.824 1.29 1.39 0.0336 0.202
## 2003 9.213 1.33 1.41 0.3186 0.204
## 2004 8.653 1.35 1.44 0.3126 0.207
## 2005 4.196 1.54 1.47 0.1978 0.211
## 2006 5.843 1.51 1.51 0.2675 0.214
## 2007 5.417 1.55 1.53 0.2419 0.216
## 2008 2.436 1.62 1.55 0.1217 0.217
## 2009 2.711 1.66 1.56 0.1396 0.216
## 2010 13.779 1.26 1.57 0.4161 0.215
## 2011 3.369 1.66 1.57 0.1669 0.215
winter_2010_flux <- winter$`FN Flux [10^6kg/yr]`[winter$Year == 2010]
filter_setPA <- function(Daily, paStart, paLong){
monthsToUse <- seq(from = paStart,
by = 1,
length.out = paLong)
monthsToUse[monthsToUse > 12] <- monthsToUse[monthsToUse > 12] - 12
Daily_filtered <- Daily %>%
filter(Month %in% monthsToUse) %>%
mutate(YearIndex = trunc(DecYear))
crossesYear <- paLong + (paStart - 1) > 12
if(crossesYear){
Daily_filtered$YearIndex[Daily_filtered$Month >= paStart] <-
Daily_filtered$YearIndex[Daily_filtered$Month >= paStart] + 1
}
get_years <- Daily_filtered %>%
group_by(YearIndex) %>%
mutate(Year = trunc(mean(DecYear))) %>%
ungroup()
return(get_years)
}
number_of_days <- eList$Daily %>%
filter_setPA(paStart = eList$INFO$paStart,
paLong = eList$INFO$paLong) %>%
group_by(Year) %>%
summarise(n_days = sum(!is.na(Q)))
number_of_days_2010 <- number_of_days$n_days[number_of_days$Year == 2010]Note that now the estimated flow normalized flux is 0.215 106 kg/year. Let’s take a moment to think about that in relation to the previous result. What it is saying is that the flux (mass per unit time) is greater during this three month period that the average flux for the entire water year. That makes sense, some seasons will have higher than average fluxes and other seasons will have lower than average fluxes.
Now, it might be that we want to think about these results, not in terms of a flux but in terms of mass alone. In the first result (water year) the mass for the year is 0.149 106 kg. But for the winter season we would compute the mass as 0.215 * 90 / 365 to give us a result of 0.053 106 kg. To get this result we took the annual rate (0.215) and divided by the number of days in the year (365) to get a rate in mass per day and then multiplied by the number of days in the season (90) which is the sum of the length of those three months to simply get a total mass.
We have taken pains here to run through this calculation because users have sometimes been confused, wondering how the flux for a part of the year can be greater than the flux for the whole year. Depending on the ultimate objective of the analysis one might want to present the seasonal results in either of these ways (mass or mass per unit time).
Next we will look at descriptions of change.
Seasonal Changes
Let’s use the tableChange function to explore the change from 1990 to 2010. We will do it first for the full water year and then for the winter season.
eList <- setPA(eList, paStart = 12, paLong = 12)
change_annual_flux <- tableChangeSingle(eList, flux = TRUE,
yearPoints = c(1990,2010))##
## Choptank River
## Inorganic nitrogen (nitrate and nitrite)
## Year Starting With December
##
##
##
## Flux Trends
## time span change slope change slope
## 10^6 kg/yr 10^6 kg/yr/yr % %/yr
##
## 1990 to 2010 0.02 0.00099 15 0.77
change_annual_conc <- tableChangeSingle(eList, flux = FALSE,
yearPoints = c(1990,2010))##
## Choptank River
## Inorganic nitrogen (nitrate and nitrite)
## Year Starting With December
##
## Concentration trends
## time span change slope change slope
## mg/L mg/L/yr % %/yr
##
## 1990 to 2010 0.32 0.016 28 1.4
eList <- setPA(eList, paStart = 12, paLong = 3)
change_season_flux <- tableChangeSingle(eList, flux = TRUE,
yearPoints = c(1990,2010))##
## Choptank River
## Inorganic nitrogen (nitrate and nitrite)
## Season Consisting of Dec Jan Feb
##
##
##
## Flux Trends
## time span change slope change slope
## 10^6 kg/yr 10^6 kg/yr/yr % %/yr
##
## 1990 to 2010 0.02 0.001 10 0.51
change_season_conc <- tableChangeSingle(eList, flux = FALSE,
yearPoints = c(1990,2010))##
## Choptank River
## Inorganic nitrogen (nitrate and nitrite)
## Season Consisting of Dec Jan Feb
##
## Concentration trends
## time span change slope change slope
## mg/L mg/L/yr % %/yr
##
## 1990 to 2010 0.24 0.012 18 0.89What we see is a fairly large difference between the concentration trends for the winter as compared to the whole year (concentration rose more steeply for the winter than it did for the year on average). But what we are going to focus on here is the trend in flux. The first thing to note is that the change from 1990 to 2010 is identical for the winter season and the year as a whole. That is, the change in the flow normalized flux for the full water year is 0.02 106 kg/year (it went from 0.129 to 0.149) and then, when we look at the winter season the change is also 0.02 106 kg/yr (from 0.195 to 0.215). So the change for this season over the 20 year period is essentially the same as the change for the entire water year. In other words, the results tell us that although the change in flux (mass per unit time) for the winter is the same as for the full year, the change in the mass for the winter season is about 25% of the change for the full year (because the winter consists of about 25% of the days in the year). Thus, we can conclude that the winter change is not atypical of the changes for the other parts of the year.
The results shown above also express the change as a slope (either
0.00099 or 0.001 virtually identical to each other) and these are simply
the change results divided by the number of years. The next entry in the
tableChange output is for change expressed as %. Here we
see a big difference between the winter and the whole year. The whole
year shows an increase of 15 % over the 20 years, while the winter
season shows an increase of 10 %. That is because the same amount of
increase 0.02 106 kg / year is being compared to a the
smaller number (1990 flow normalized annual flux of 0.129 106
kg/year) in the first table and compared to a larger number (seasonal
flux of 0.195 106 kg/year) in the second table. So, even
though the change is focused equally in the winter and non-winter
months, the percentage change for the winter is smaller than the
percentage change for the whole year.
Seasonal Load Fraction
Next, we can think about the seasonal load fraction.
You will need to read in two new functions called
setupSeasons and setupYearsPlus designed for
this purpose. You can copy them from here and paste them into your
workspace (all as a single copy and paste) or you can create an .R file
from them that you will source each time you want to use them. The
functions use the package dplyr,
a package that is useful for general data exploration and
manipulation.
setupSeasons <- function(eList){
Daily <- eList$Daily
paLong <- eList$INFO$paLong
paStart <- eList$INFO$paStart
Daily_season <- filter_setPA(Daily,
paStart = paStart,
paLong = paLong)
Daily_annual <- filter_setPA(Daily,
paStart = paStart,
paLong = 12)
#Cleanup units:
divideBy <- 1000000
divideBy <- 1
# Convert flux to kg/year
unit_scale <- fluxConst[[9]]@unitFactor / divideBy
SeasonResults <- Daily_season %>%
group_by(Year) %>%
summarize(DecYear = mean(DecYear),
Counts = sum(!is.na(ConcDay)),
Flux = mean(FluxDay) * unit_scale,
FNFlux = mean(FNFlux) * unit_scale)
AnnualResults <- Daily_annual %>%
group_by(Year) %>%
summarize(AnnualCounts = sum(!is.na(ConcDay)),
AnnualFlux = mean(FluxDay) * unit_scale,
AnnualFNFlux = mean(FNFlux) * unit_scale) %>%
filter(AnnualCounts >= 365)
seasonPctResults <- SeasonResults %>%
select(DecYear, Year, Flux, FNFlux, Counts) %>%
left_join(select(AnnualResults,
Year, AnnualCounts,
AnnualFlux, AnnualFNFlux), by="Year") %>%
filter(!is.na(AnnualFlux)) %>%
mutate(pctFlux = 100*Flux*Counts/(AnnualFlux*AnnualCounts),
pctFNFlux = 100*FNFlux*Counts/(AnnualFNFlux*AnnualCounts)) %>%
rename(SeasonFlux = Flux,
SeasonFNFlux = FNFlux)
return(seasonPctResults)
}Simply use the loaded eList to calculate these seasonal
load fractions. Let’s go back to the winter season (Dec-Feb):
eList <- setPA(eList, paStart = 12, paLong = 3)
seasonPctResults <- setupSeasons(eList)Looking at your results
What you now have is a data frame called
seasonPctResults. The columns it contains are the
following:
| variable | Definition |
|---|---|
| DecYear | Decimal Year of the mid-date of the season |
| Year | Calendar Year of mid-date of the year |
| AnnualFlux | Estimated flux for the water year in millions of kg |
| AnnualFNFlux | Flow Normalized flux for the water year in millions of kg |
| SeasonFlux | Estimated flux for the season in millions of kg |
| SeasonFNFlux | Flow Normalized flux for the season in millions of kg |
| pctFlux | Season flux as a percentage of Annual Flux |
| pctFNFlux | FlowNormalized Seasonal Flux as a percent of Flow Normalized Annual Flux |
Plotting the time series
We can make a graph showing the percentage flux (estimated annual and
flow normalized). Note, this workflow uses base R plotting functions.
You could also use the EGRET function
genericEGRETDotPlot to automatically to pick some plotting
styles that are consistent with other EGRET plots.
plotTitle = paste("Seasonal Flux as a Percent of Annual Flux\n",
eList$INFO$shortName, eList$INFO$paramShortName,
"\nSolid line is percentage of flow normalized flux")
par(mar=c(5,6,4,2) + 0.1,mgp=c(3,1,0))
plot(seasonPctResults$DecYear, seasonPctResults$pctFlux,pch=20,
yaxs="i",ylim = c(0,100),las=1,tck=.01,
xlab="Year",ylab="Percentage of Annual Flux",
main=plotTitle,cex=1.5)
lines(seasonPctResults$DecYear,seasonPctResults$pctFNFlux,col="green",lwd=2)
axis(3, labels = FALSE,tck=.01)
axis(4, labels = FALSE,tck=.01)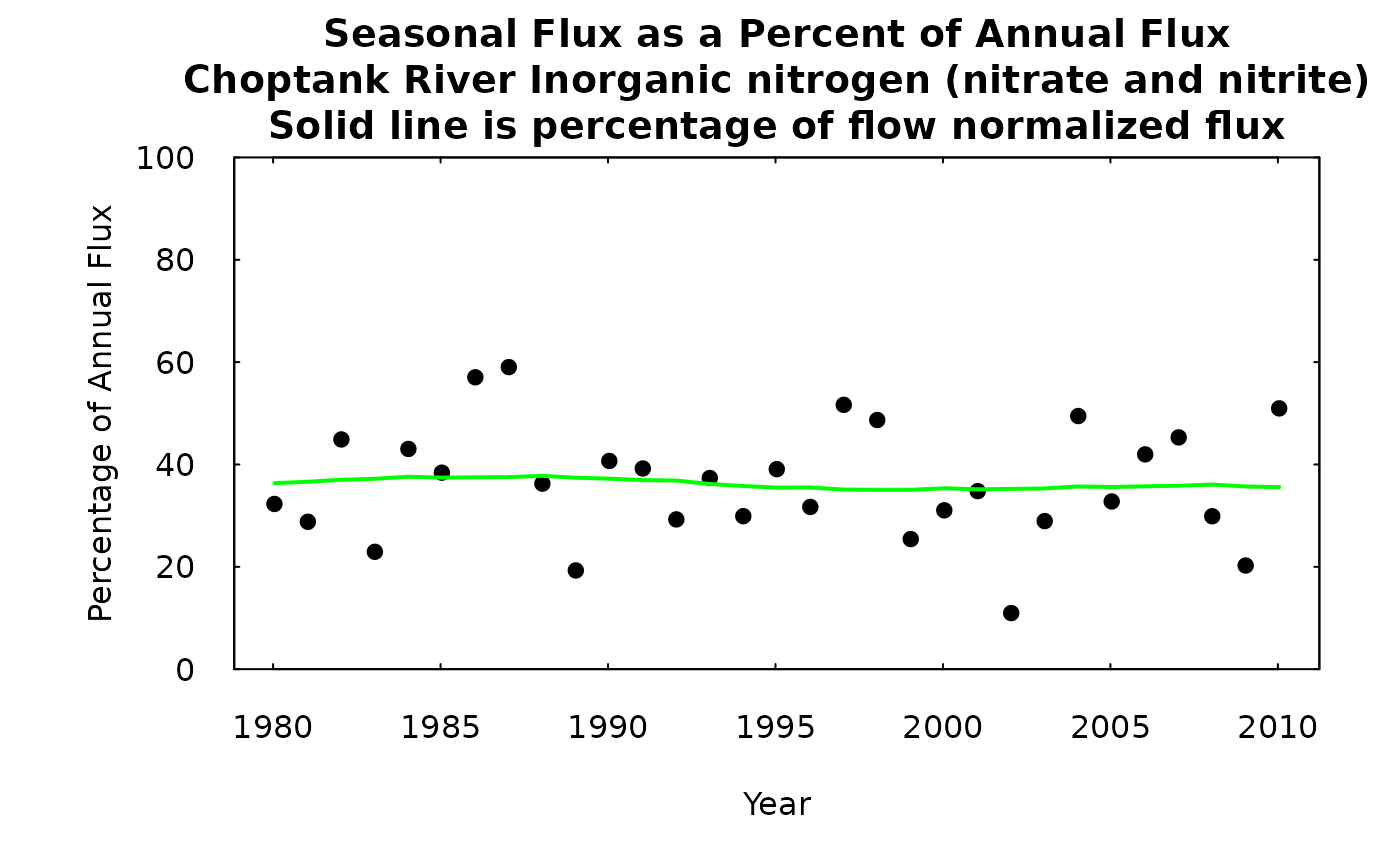
Seasonal flux as a percentage of annual flux.
We can interpret this example graph as follows. The winter flux of Inorganic nitrogen (nitrate and nitrite) fluctuates a good deal from year to year. From a low of around 10% to a high of around 60% but the mean percentage hasn’t changed much over the years. It is around 35% of the annual total flux.
Computing averages over a period of years
Let’s say we wanted to answer the question, what percentage of the annual total flux moved in the winter season during the years 2000 through 2010. We can answer that question with a simple set of calculations.
Keep in mind, the way we are defining “year” is what year the ending year of the period of anaylsis fell. So, for this analysis, the full 2010 “year” is from Dec. 2009 through the end of November 2010.
Filter the data frame
seasonPctResultsfor the years 2000 - 2010.Now we can compute the sum of the annual fluxes for those years and the sum of the seasonal fluxes for those years, and then get our answer by taking the ratio and multiplying by 100.
years00_10 <- filter(seasonPctResults, Year >= 2000, Year <= 2010)
sumYears <- sum(years00_10$AnnualFlux)
sumSeasons <- sum(years00_10$SeasonFlux * years00_10$Counts /
years00_10$AnnualCounts)
avePct <- 100 * sumSeasons / sumYearsThe total flux for all years in the period of interest in millions of
kg is sumYears = 1.73.
The total seasonal flux for all years of the period of interest in
millions of kg is sumSeasons = 0.61.
The percentage of the total flux for the years 2000 through 2010 that
was transported in the winter months is avePct = 35.3.
This can be determined for any set of years simply by changing
Year values in the dplyr::filter function. So,
for the years 1990-1999:
years90_99 <- filter(seasonPctResults, Year >= 1990, Year <= 1999)
c("sumYears" = sum(years90_99$AnnualFlux),
"sumSeasons" = sum(years90_99$SeasonFlux * years90_99$Counts / years90_99$AnnualCounts),
"avePct" = 100 * sumSeasons / sumYears)## sumYears sumSeasons avePct
## 1.3327152 0.5037539 35.2611821