This function computes the first day of the calendar year at which a specific fraction of the cumulative flow for that year has been exceeded. Typically one looks for the point where half the cumulative flow has happened (fract = 0.5). The portion of the year being considered is set by paStart and paLong. The matrix returned has 2 columns: the first is the year (integer when the period of analysis ends), the second is the day of the year when the fraction has been exceeded. None of the rows will have any NA values.
Arguments
- eList
named list with at least the Sample and INFO dataframes
- paStart
numeric integer specifying the starting month for the period of analysis, 1 <= paStart <= 12, default is 10
- paLong
numeric integer specifying the length of the period of analysis, in months, 1 <= paLong <= 12, default is 12
- fract
numeric fraction of the flow
Value
annualSeries an integer matrix of two columns. The first column is the calendar year for the end of the period The second column is day of the year when the flow has exceeded the specified fraction of the entire period being considered
Details
It is common to use this type of analysis on the snowmelt period of the year. If (for example) we assume that snowmelt starts with the month of March and ends in July then we would set paStart = 3 and paLong = 5
Examples
eList <- Choptank_eList
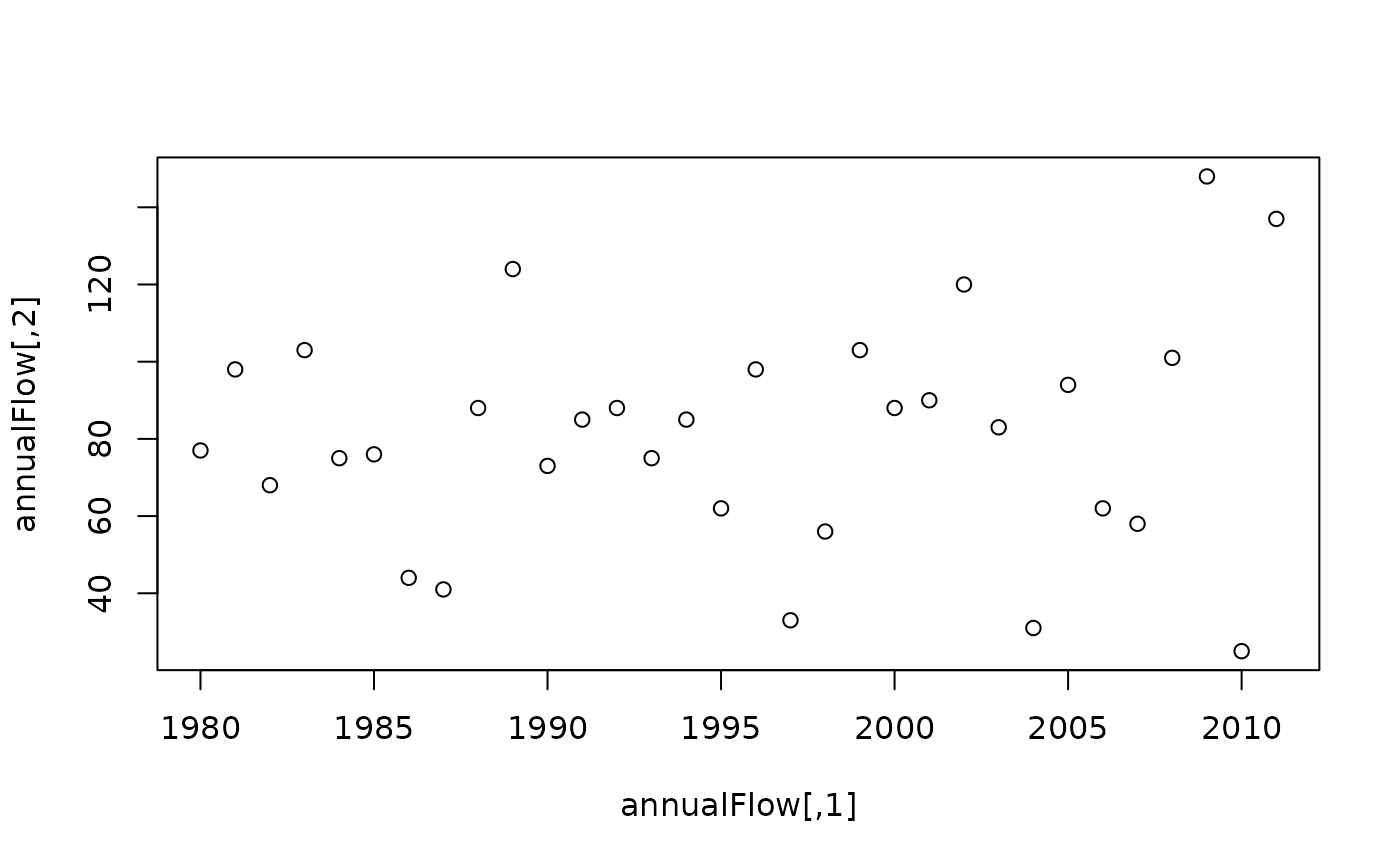
annualFlow <- cumQdate(eList)
head(annualFlow)
#> [,1] [,2]
#> [1,] 1980 77
#> [2,] 1981 98
#> [3,] 1982 68
#> [4,] 1983 103
#> [5,] 1984 75
#> [6,] 1985 76
plot(annualFlow)
mod1 <- stats::lm(annualFlow[,2] ~ annualFlow[,1])
summary(mod1)
#>
#> Call:
#> stats::lm(formula = annualFlow[, 2] ~ annualFlow[, 1])
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -61.022 -19.700 3.093 15.992 62.331
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -623.1512 1128.3270 -0.552 0.585
#> annualFlow[, 1] 0.3528 0.5654 0.624 0.537
#>
#> Residual standard error: 29.53 on 30 degrees of freedom
#> Multiple R-squared: 0.01281, Adjusted R-squared: -0.02009
#> F-statistic: 0.3894 on 1 and 30 DF, p-value: 0.5374
#>