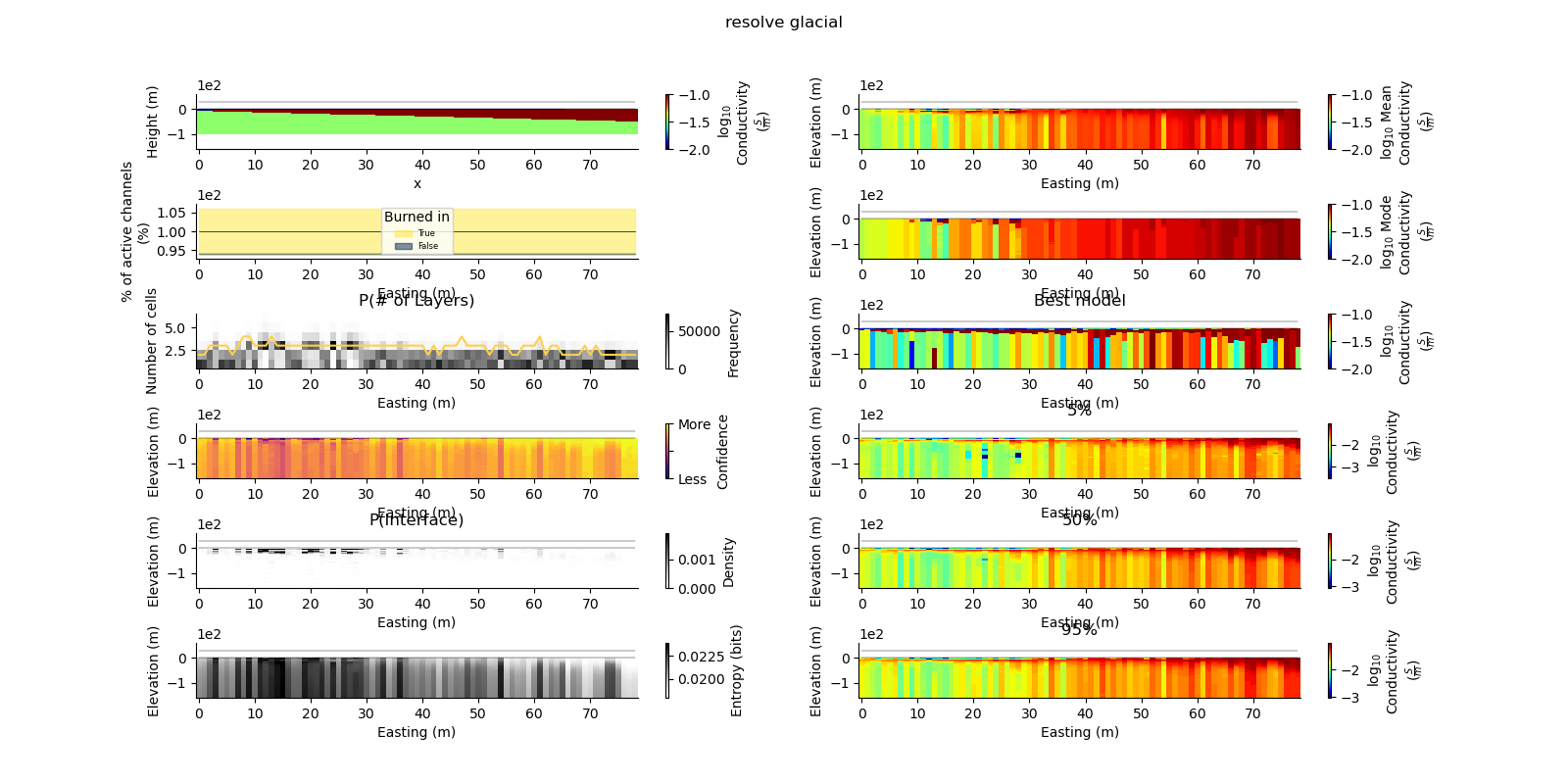
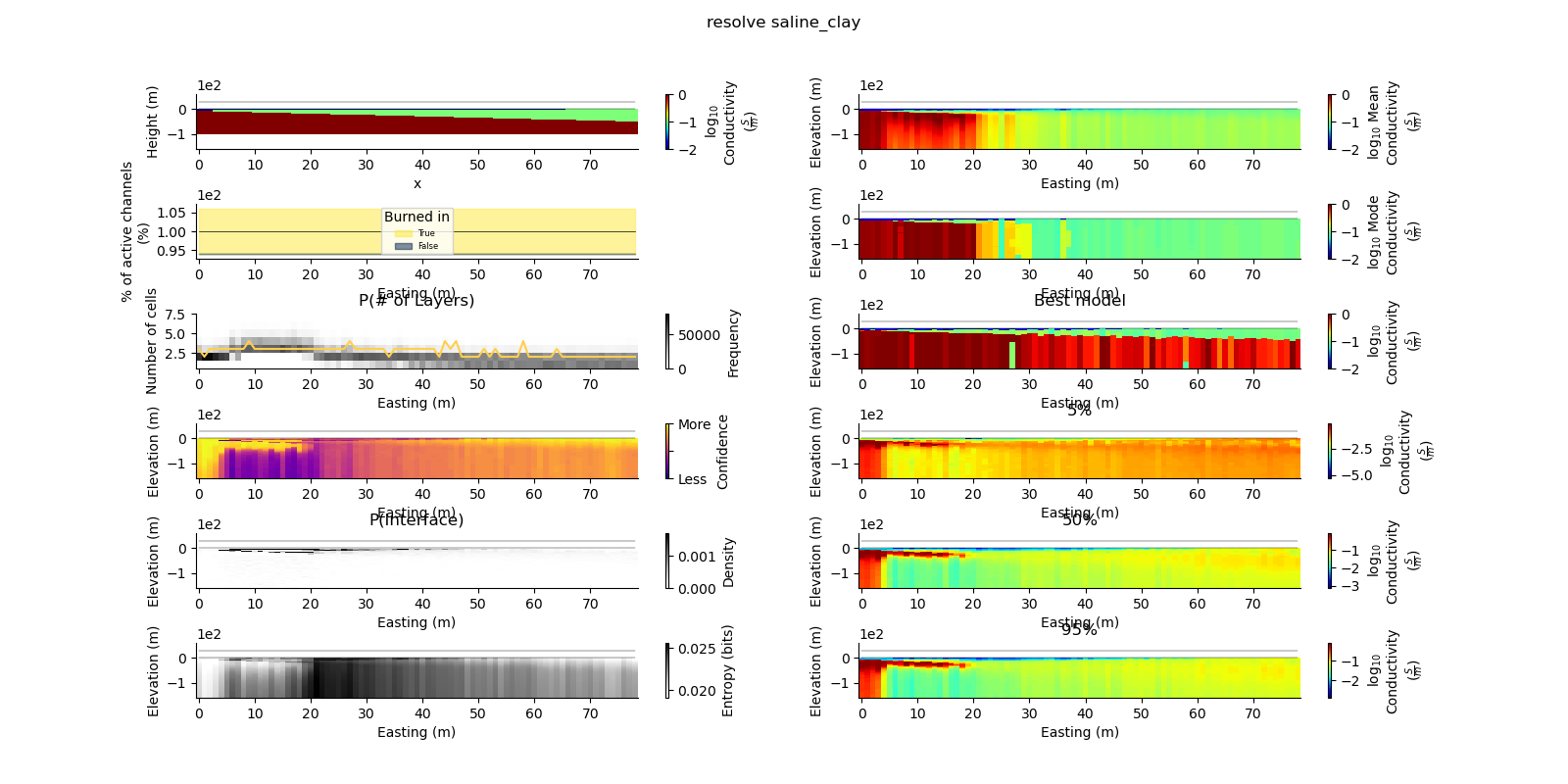
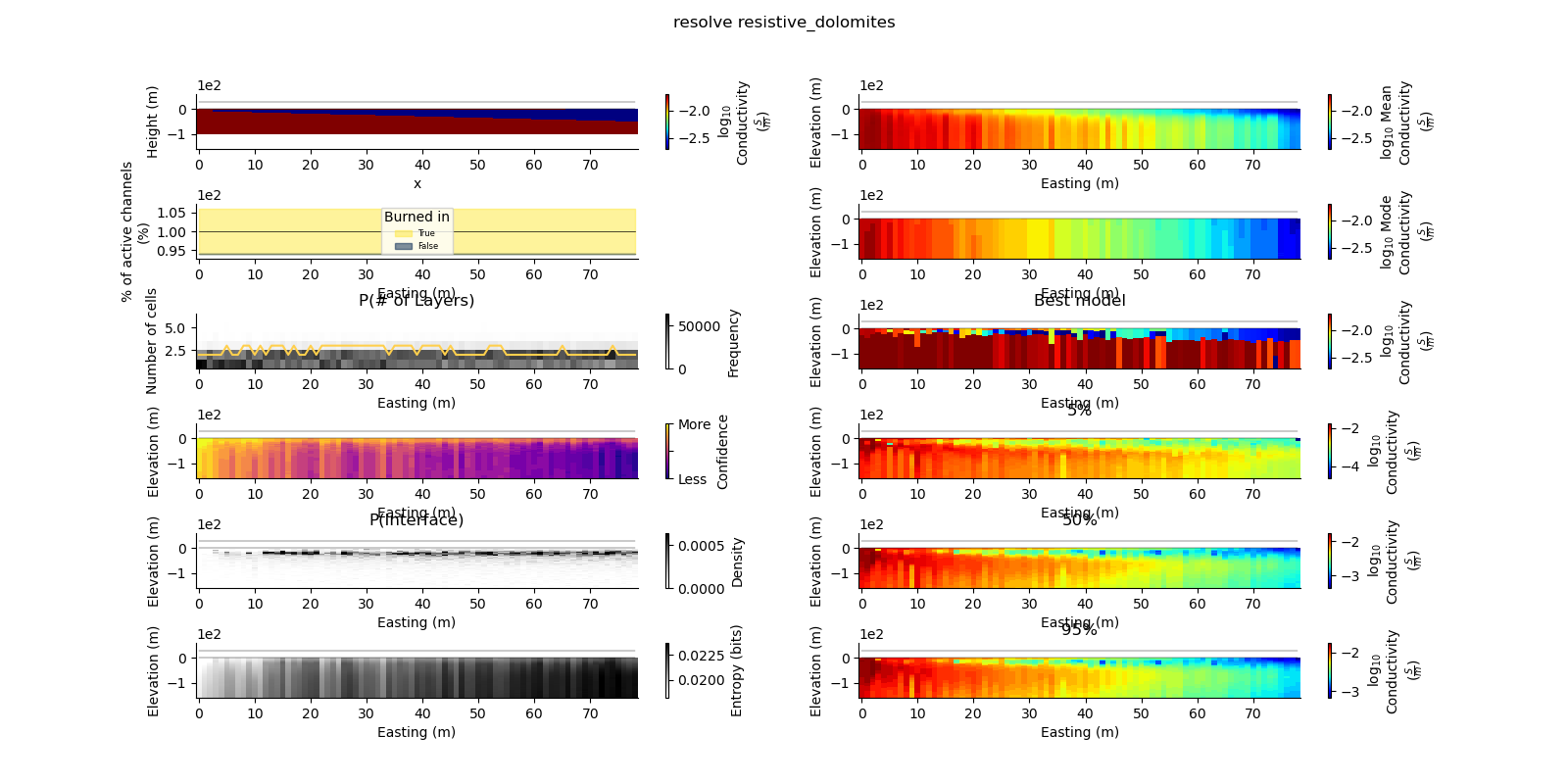
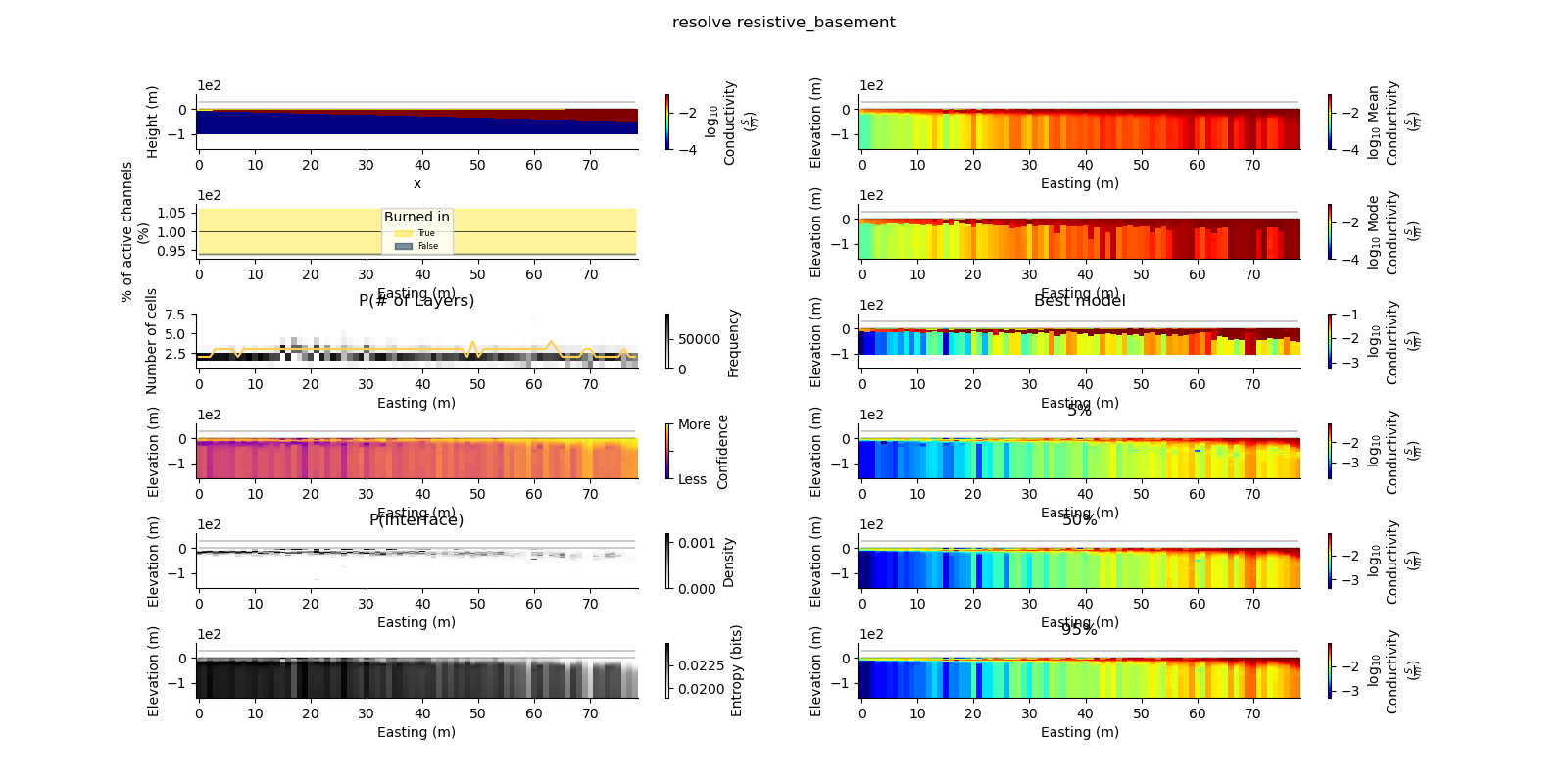
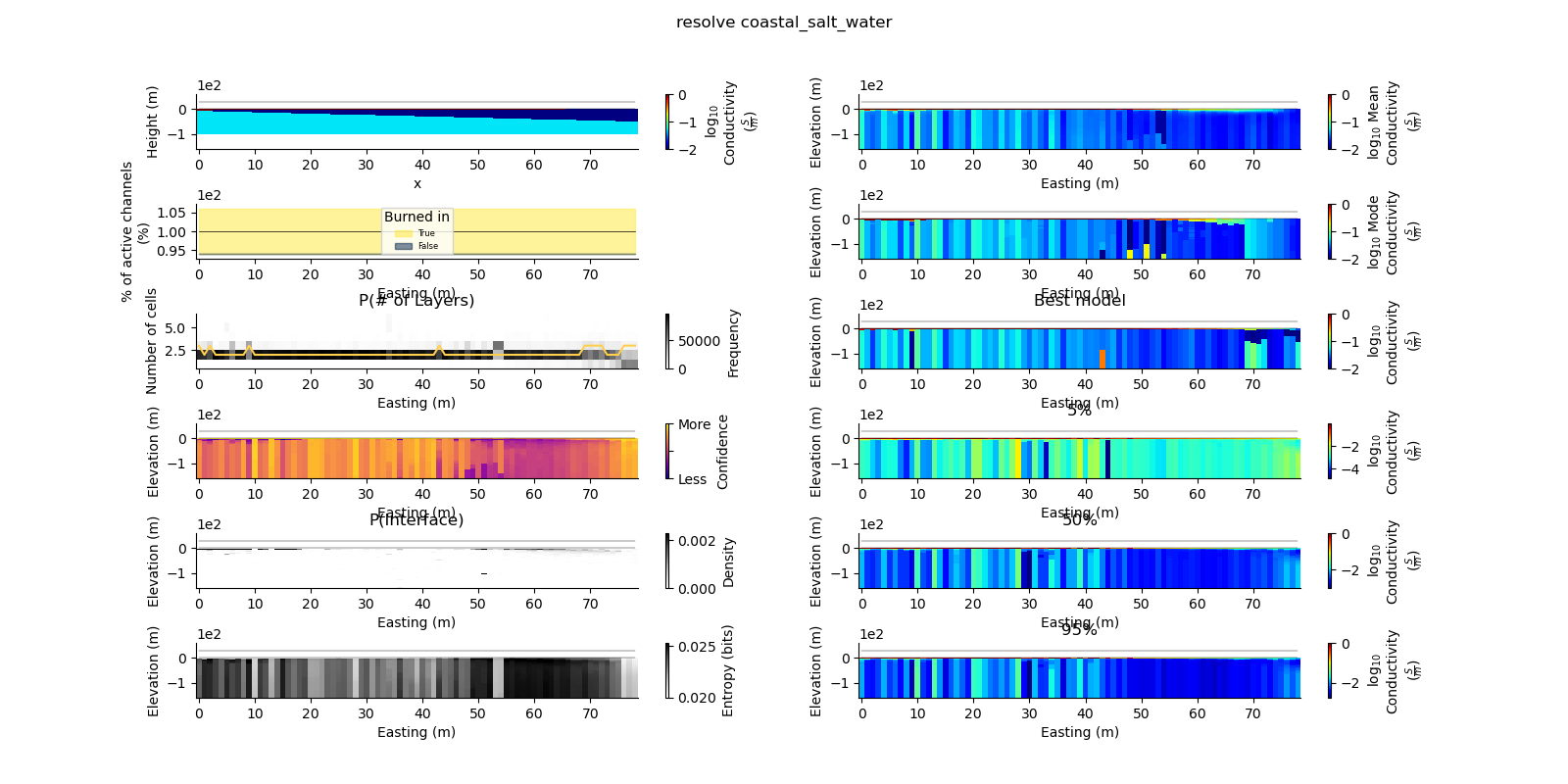
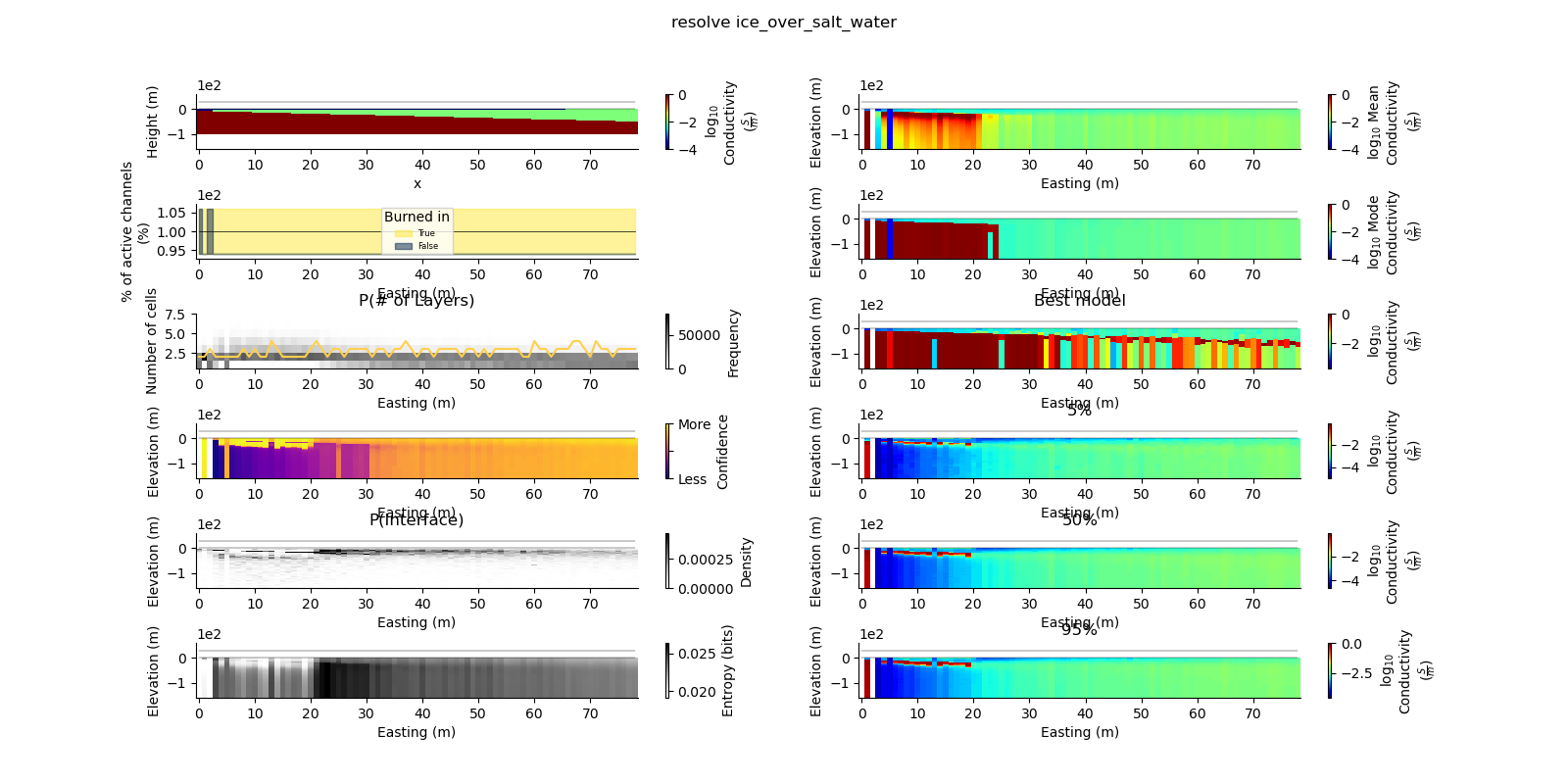
2D Posterior analysis of Resolve inference

All plotting in GeoBIPy can be carried out using the 3D inference class

• 
• 
• 
• 
• 
• 

import matplotlib.pyplot as plt
import numpy as np
from geobipy import Model
from geobipy import Inference2D

def plot_2d_summary(folder, data_type, model_type):
   #%%
   # Inference for a line of inferences
   # ++++++++++++++++++++++++++++++++++
   #
   # We can instantiate the inference handler by providing a path to the directory containing
   # HDF5 files generated by GeoBIPy.
   #
   # The InfereceXD classes are low memory.  They only read information from the HDF5 files
   # as and when it is needed.
   #
   # The first time you use these classes to create plots, expect longer initial processing times.
   # I precompute expensive properties and store them in the HDF5 files for later use.

   from numpy.random import Generator
   from numpy.random import PCG64DXSM
   generator = PCG64DXSM(seed=0)
   prng = Generator(generator)

   #%%
   results_2d = Inference2D.fromHdf('{}/{}/{}/0.0.h5'.format(folder, data_type, model_type), prng=prng)

   kwargs = {
         "log" : 10,
         "cmap" : 'jet'
         }

   fig = plt.figure(figsize=(16, 8))
   plt.suptitle("{} {}".format(data_type, model_type))
   gs0 = fig.add_gridspec(6, 2, hspace=1.0)

   true_model = Model.create_synthetic_model(model_type)
   true_model.mesh.y_edges = true_model.mesh.y_edges / 10.0

   kwargs['vmin'] = np.log10(np.min(true_model.values))
   kwargs['vmax'] = np.log10(np.max(true_model.values))

   ax = fig.add_subplot(gs0[0, 0])
   true_model.pcolor(flipY=True, ax=ax, wrap_clabel=True, **kwargs)
   results_2d.plot_data_elevation(linewidth=0.3, ax=ax, xlabel=False, ylabel=False);
   results_2d.plot_elevation(linewidth=0.3, ax=ax, xlabel=False, ylabel=False);

   plt.ylim([-160, 60])

   ax1 = fig.add_subplot(gs0[0, 1], sharex=ax, sharey=ax)
   results_2d.plot_mean_model(ax=ax1, wrap_clabel=True, **kwargs);
   results_2d.plot_data_elevation(linewidth=0.3, ax=ax1);
   results_2d.plot_elevation(linewidth=0.3, ax=ax1);

   # By adding the useVariance keyword, we can make regions of lower confidence more transparent
   ax1 = fig.add_subplot(gs0[1, 1], sharex=ax, sharey=ax)
   results_2d.plot_mode_model(ax=ax1, wrap_clabel=True, **kwargs);
   results_2d.plot_data_elevation(linewidth=0.3, ax=ax1);
   results_2d.plot_elevation(linewidth=0.3, ax=ax1);

   # # # # # We can also choose to keep parameters above the DOI opaque.
   # # # # results_2d.compute_doi()
   # # # # plt.subplot(313)
   # # # # results_2d.plot_mean_model(use_variance=True, mask_below_doi=True, **kwargs);
   # # # # results_2d.plot_data_elevation(linewidth=0.3);
   # # # # results_2d.plot_elevation(linewidth=0.3);

   ax1 = fig.add_subplot(gs0[2, 1], sharex=ax, sharey=ax)
   results_2d.plot_best_model(ax=ax1, wrap_clabel=True, **kwargs);
   results_2d.plot_data_elevation(linewidth=0.3, ax=ax1);
   results_2d.plot_elevation(linewidth=0.3, ax=ax1);
   ax1.set_title('Best model')

   del kwargs['vmin']
   del kwargs['vmax']

   ax1 = fig.add_subplot(gs0[3, 1], sharex=ax, sharey=ax); ax1.set_title('5%')
   results_2d.plot_percentile(ax=ax1, percent=0.05, wrap_clabel=True, **kwargs)
   results_2d.plot_data_elevation(linewidth=0.3, ax=ax1);
   results_2d.plot_elevation(linewidth=0.3, ax=ax1);

   ax1 = fig.add_subplot(gs0[4, 1], sharex=ax, sharey=ax); ax1.set_title('50%')
   results_2d.plot_percentile(ax=ax1, percent=0.5, wrap_clabel=True, **kwargs)
   results_2d.plot_data_elevation(linewidth=0.3, ax=ax1);
   results_2d.plot_elevation(linewidth=0.3, ax=ax1);

   ax1 = fig.add_subplot(gs0[5, 1], sharex=ax, sharey=ax); ax1.set_title('95%')
   results_2d.plot_percentile(ax=ax1, percent=0.95, wrap_clabel=True, **kwargs)
   results_2d.plot_data_elevation(linewidth=0.3, ax=ax1);
   results_2d.plot_elevation(linewidth=0.3, ax=ax1);

   #%%
   # We can plot the parameter values that produced the highest posterior
   ax1 = fig.add_subplot(gs0[2, 0], sharex=ax)
   results_2d.plot_k_layers(ax=ax1, wrap_ylabel=True)

   ax1 = fig.add_subplot(gs0[1, 0], sharex=ax)

   ll, bb, ww, hh = ax1.get_position().bounds
   ax1.set_position([ll, bb, ww*0.8, hh])

   results_2d.plot_channel_saturation(ax=ax1, wrap_ylabel=True)
   results_2d.plot_burned_in(ax=ax1, underlay=True)

   #%%
   # Now we can start plotting some more interesting posterior properties.
   # How about the confidence?
   ax1 = fig.add_subplot(gs0[3, 0], sharex=ax, sharey=ax)
   results_2d.plot_confidence(ax=ax1);
   results_2d.plot_data_elevation(ax=ax1, linewidth=0.3);
   results_2d.plot_elevation(ax=ax1, linewidth=0.3);

   #%%
   # We can take the interface depth posterior for each data point,
   # and display an interface probability cross section
   # This posterior can be washed out, so the clim_scaling keyword lets me saturate
   # the top and bottom 0.5% of the colour range
   ax1 = fig.add_subplot(gs0[4, 0], sharex=ax, sharey=ax)
   ax1.set_title('P(Interface)')
   results_2d.plot_interfaces(cmap='Greys', clim_scaling=0.5, ax=ax1);
   results_2d.plot_data_elevation(linewidth=0.3, ax=ax1);
   results_2d.plot_elevation(linewidth=0.3, ax=ax1);

   ax1 = fig.add_subplot(gs0[5, 0], sharex=ax, sharey=ax)
   results_2d.plot_entropy(cmap='Greys', clim_scaling=0.5, ax=ax1);
   results_2d.plot_data_elevation(linewidth=0.3, ax=ax1);
   results_2d.plot_elevation(linewidth=0.3, ax=ax1);


   plt.show()
   # plt.savefig('{}_{}.png'.format(data_type, model_type), dpi=300)

if __name__ == '__main__':
   models = ['glacial', 'saline_clay', 'resistive_dolomites', 'resistive_basement', 'coastal_salt_water', 'ice_over_salt_water']

   for model in models:
      try:
         plot_2d_summary("../../../Parallel_Inference/", "resolve", model)
      except Exception as e:
         print(model)
         print(e)
         pass