08: Working with tabular data in Pandas

6dc5f9ca06e641cdb7b8f99a151accf9

Not that type of Panda – Python’s Pandas package

Pandas is a powerful, flexible and easy to use open source data analysis and manipulation tool. Pandas is commonly used for operations that would normally be done in a spreadsheet environment and includes powerful data analysis and manipulation tools.

Let’s begin by importing the libraries and setting our data path

[1]:

from pathlib import Path
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
import statsmodels.api as sm
from dataretrieval import nwis
from matplotlib.backends.backend_pdf import PdfPages
from scipy.signal import detrend

data_path = Path("..", "data", "pandas")

Get site information data for part of the Russian River near Guerneville, CA from NWIS

[2]:

bbox = (-123.10, 38.45, -122.90, 38.55)
info, metadata = nwis.get_info(bBox=[str(i) for i in bbox])
if 'geometry' in list(info):
    # dataretreival now returns as geopandas dataframe, drop "geometry" column for this example
    info.drop(columns=["geometry"], inplace=True)

[3]:

info.to_csv(data_path / "site_info.csv", index=False)
info.head()

[3]:

	agency_cd	site_no	station_nm	site_tp_cd	lat_va	long_va	dec_lat_va	dec_long_va	coord_meth_cd	coord_acy_cd	...	local_time_fg	reliability_cd	gw_file_cd	nat_aqfr_cd	aqfr_cd	aqfr_type_cd	well_depth_va	hole_depth_va	depth_src_cd	project_no
0	USGS	11467000	RUSSIAN R A HACIENDA BRIDGE NR GUERNEVILLE CA	ST	383031.0	1225536.0	38.508482	-122.927734	M	F	...	Y	NaN	NNNNNNNN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
1	USGS	11467002	RUSSIAN R A JOHNSONS BEACH A GUERNEVILLE CA	ST	382958.0	1225950.0	38.499358	-122.998333	M	F	...	Y	NaN	NNNNNNNN	NaN	NaN	NaN	NaN	NaN	NaN	967760420
2	USGS	11467006	RUSSIAN R A VACATION BEACH CA	ST	382903.0	1230041.0	38.484080	-123.012500	M	F	...	Y	NaN	NNNNNNNN	NaN	NaN	NaN	NaN	NaN	NaN	967760420
3	USGS	11467050	BIG AUSTIN C A CAZADERO CA	ST	383215.0	1230518.0	38.537413	-123.089447	M	F	...	Y	NaN	NNNNNNNN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
4	USGS	11467200	AUSTIN C NR CAZADERO CA	ST	383024.0	1230407.0	38.506536	-123.069683	M	S	...	Y	NaN	NNNNNNNN	NaN	NaN	NaN	NaN	NaN	NaN	967700102

5 rows × 42 columns

Wow that’s a lot of gages in this location, let’s info on all of them and then use this data to learn about pandas

The data returned to us from our NWIS query info was returned to us as pandas DataFrame. We’ll be working with this to start learning about the basics of pandas.

Viewing data in pandas

Pandas has built in methods to inspect DataFrame objects. We’ll look at a few handy methods:

.head(): inspect the first few rows of data
.tail(): inspect the last few rows of data
.index(): show the row indexes
.columns(): show the column names
.describe(): statistically describe the data

[4]:

info.head()

[4]:

	agency_cd	site_no	station_nm	site_tp_cd	lat_va	long_va	dec_lat_va	dec_long_va	coord_meth_cd	coord_acy_cd	...	local_time_fg	reliability_cd	gw_file_cd	nat_aqfr_cd	aqfr_cd	aqfr_type_cd	well_depth_va	hole_depth_va	depth_src_cd	project_no
0	USGS	11467000	RUSSIAN R A HACIENDA BRIDGE NR GUERNEVILLE CA	ST	383031.0	1225536.0	38.508482	-122.927734	M	F	...	Y	NaN	NNNNNNNN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
1	USGS	11467002	RUSSIAN R A JOHNSONS BEACH A GUERNEVILLE CA	ST	382958.0	1225950.0	38.499358	-122.998333	M	F	...	Y	NaN	NNNNNNNN	NaN	NaN	NaN	NaN	NaN	NaN	967760420
2	USGS	11467006	RUSSIAN R A VACATION BEACH CA	ST	382903.0	1230041.0	38.484080	-123.012500	M	F	...	Y	NaN	NNNNNNNN	NaN	NaN	NaN	NaN	NaN	NaN	967760420
3	USGS	11467050	BIG AUSTIN C A CAZADERO CA	ST	383215.0	1230518.0	38.537413	-123.089447	M	F	...	Y	NaN	NNNNNNNN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
4	USGS	11467200	AUSTIN C NR CAZADERO CA	ST	383024.0	1230407.0	38.506536	-123.069683	M	S	...	Y	NaN	NNNNNNNN	NaN	NaN	NaN	NaN	NaN	NaN	967700102

5 rows × 42 columns

[5]:

info.tail()

[5]:

	agency_cd	site_no	station_nm	site_tp_cd	lat_va	long_va	dec_lat_va	dec_long_va	coord_meth_cd	coord_acy_cd	...	local_time_fg	reliability_cd	gw_file_cd	nat_aqfr_cd	aqfr_cd	aqfr_type_cd	well_depth_va	hole_depth_va	depth_src_cd	project_no
23	USGS	383012122574501	RUSSIAN R A ODD FELLOWS PARK NR RIO NIDO CA	ST	383012.0	1225745.0	38.503333	-122.962500	G	F	...	Y	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	967760420
24	USGS	383016123041101	008N011W27N001M	GW	383016.3	1230411.0	38.504528	-123.069722	G	5	...	Y	C	YY Y	NaN	NaN	NaN	30.0	30.0	D	00BHM8187
25	USGS	383017122580301	008N010W28RU01M	GW	383017.4	1225802.5	38.504833	-122.967361	G	5	...	Y	C	YY	NaN	NaN	NaN	98.0	107.0	D	NaN
26	USGS	383028122554501	HOBSON C NR HACIENDA CA	ST	383028.0	1225545.0	38.507778	-122.929167	G	U	...	Y	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	967760420
27	USGS	383034122590701	008N010W29H004M	GW	383034.4	1225907.9	38.509556	-122.985528	G	5	...	Y	C	YY Y	N100CACSTL	NaN	NaN	99.0	110.0	D	9677BHM32

5 rows × 42 columns

[6]:

# print the index names
print(info.index)

RangeIndex(start=0, stop=28, step=1)

[7]:

# print the column names
print(info.columns)

# print the column names as a list
print(list(info))

Index(['agency_cd', 'site_no', 'station_nm', 'site_tp_cd', 'lat_va', 'long_va',
       'dec_lat_va', 'dec_long_va', 'coord_meth_cd', 'coord_acy_cd',
       'coord_datum_cd', 'dec_coord_datum_cd', 'district_cd', 'state_cd',
       'county_cd', 'country_cd', 'land_net_ds', 'map_nm', 'map_scale_fc',
       'alt_va', 'alt_meth_cd', 'alt_acy_va', 'alt_datum_cd', 'huc_cd',
       'basin_cd', 'topo_cd', 'instruments_cd', 'construction_dt',
       'inventory_dt', 'drain_area_va', 'contrib_drain_area_va', 'tz_cd',
       'local_time_fg', 'reliability_cd', 'gw_file_cd', 'nat_aqfr_cd',
       'aqfr_cd', 'aqfr_type_cd', 'well_depth_va', 'hole_depth_va',
       'depth_src_cd', 'project_no'],
      dtype='str')
['agency_cd', 'site_no', 'station_nm', 'site_tp_cd', 'lat_va', 'long_va', 'dec_lat_va', 'dec_long_va', 'coord_meth_cd', 'coord_acy_cd', 'coord_datum_cd', 'dec_coord_datum_cd', 'district_cd', 'state_cd', 'county_cd', 'country_cd', 'land_net_ds', 'map_nm', 'map_scale_fc', 'alt_va', 'alt_meth_cd', 'alt_acy_va', 'alt_datum_cd', 'huc_cd', 'basin_cd', 'topo_cd', 'instruments_cd', 'construction_dt', 'inventory_dt', 'drain_area_va', 'contrib_drain_area_va', 'tz_cd', 'local_time_fg', 'reliability_cd', 'gw_file_cd', 'nat_aqfr_cd', 'aqfr_cd', 'aqfr_type_cd', 'well_depth_va', 'hole_depth_va', 'depth_src_cd', 'project_no']

The describe() method is only useful for numerical data. This example is does not have a lot of useful data for describe(), however we’ll use it again later

[8]:

info.describe()

[8]:

	lat_va	long_va	dec_lat_va	dec_long_va	district_cd	state_cd	county_cd	map_scale_fc	alt_va	alt_acy_va	huc_cd	basin_cd	construction_dt	inventory_dt	drain_area_va	contrib_drain_area_va	aqfr_cd	aqfr_type_cd	well_depth_va	hole_depth_va
count	28.000000	2.800000e+01	28.000000	28.000000	28.0	28.0	28.0	25.0	26.000000	26.000000	2.800000e+01	0.0	6.000000e+00	1.100000e+01	6.000000	0.0	0.0	0.0	9.000000	6.00000
mean	382918.225000	1.228085e+06	38.488771	-122.993363	6.0	6.0	97.0	24000.0	41.524615	10.235385	1.931263e+10	NaN	1.987590e+07	2.009075e+07	935.400000	NaN	NaN	NaN	63.028889	76.50000
std	136.242381	2.339461e+03	0.022509	0.059290	0.0	0.0	0.0	0.0	40.057582	9.278299	5.672084e+10	NaN	5.148255e+04	5.980639e+04	691.350481	NaN	NaN	NaN	34.634297	40.79093
min	382701.000000	1.225404e+06	38.450278	-123.089447	6.0	6.0	97.0	24000.0	2.000000	0.100000	1.801011e+07	NaN	1.983093e+07	2.004091e+07	26.600000	NaN	NaN	NaN	22.000000	22.00000
25%	382795.625000	1.225627e+06	38.468229	-123.049445	6.0	6.0	97.0	24000.0	14.582500	1.600000	1.801011e+07	NaN	1.984061e+07	2.004091e+07	381.600000	NaN	NaN	NaN	30.000000	42.50000
50%	382979.950000	1.230018e+06	38.499943	-123.004861	6.0	6.0	97.0	24000.0	43.260000	4.300000	1.801011e+07	NaN	1.985078e+07	2.004092e+07	1345.500000	NaN	NaN	NaN	80.000000	93.50000
75%	383013.075000	1.230255e+06	38.503632	-122.943583	6.0	6.0	97.0	24000.0	48.000000	20.000000	1.801011e+07	NaN	1.992106e+07	2.014561e+07	1366.500000	NaN	NaN	NaN	98.000000	109.25000
max	383215.000000	1.230518e+06	38.537413	-122.901222	6.0	6.0	97.0	24000.0	211.000000	20.000000	1.801011e+11	NaN	1.994120e+07	2.017050e+07	1461.000000	NaN	NaN	NaN	99.000000	110.00000

Getting data from a pandas dataframe

There are multiple methods to get data out of a pandas dataframe as either a “series”, numpy array, or a list

Let’s start by getting data as a series using a few methods

[9]:

# get a series of site numbers by key
info["site_no"]

[9]:

0            11467000
1            11467002
2            11467006
3            11467050
4            11467200
5            11467210
6     382701123025801
7     382713123030401
8     382713123030403
9     382752123003401
10    382754123030501
11    382757123003801
12    382808122565401
13    382815123024601
14    382819123010001
15    382944123002901
16    382955122594101
17    383001122540701
18    383003122540401
19    383003122540402
20    383003122540403
21    383006123000601
22    383009122543001
23    383012122574501
24    383016123041101
25    383017122580301
26    383028122554501
27    383034122590701
Name: site_no, dtype: str

[10]:

# get station names by attribute
info.station_nm

[10]:

0     RUSSIAN R A HACIENDA BRIDGE NR GUERNEVILLE CA
1       RUSSIAN R A JOHNSONS BEACH A GUERNEVILLE CA
2                     RUSSIAN R A VACATION BEACH CA
3                        BIG AUSTIN C A CAZADERO CA
4                           AUSTIN C NR CAZADERO CA
5                      RUSSIAN R A DUNCANS MILLS CA
6                   FREEZEOUT C NR DUNCANS MILLS CA
7                                   007N011W14NU01M
8                                   007N011W14NU03M
9                       DUTCH BILL C A MONTE RIO CA
10     RUSSIAN R A CASINI RANCH NR DUNCANS MILLS CA
11                         RUSSIAN R A MONTE RIO CA
12                                  007N010W10H001M
13                     AUSTIN C NR DUNCANS MILLS CA
14                                  007N010W07D001M
15                      HULBERT C NR GUERNEVILLE CA
16                    POCKET CYN C A GUERNEVILLE CA
17                                  008N009W31C002M
18                                  008N009W31C003M
19                                  008N009W31C004M
20                                  008N009W31C005M
21                          FIFE C A GUERNEVILLE CA
22             GREEN VALLEY C NR MIRABEL HEIGHTS CA
23      RUSSIAN R A ODD FELLOWS PARK NR RIO NIDO CA
24                                  008N011W27N001M
25                                  008N010W28RU01M
26                          HOBSON C NR HACIENDA CA
27                                  008N010W29H004M
Name: station_nm, dtype: str

getting data from a dataframe as a numpy array can be accomplished by using .values

[11]:

info.station_nm.values

[11]:

<StringArray>
['RUSSIAN R A HACIENDA BRIDGE NR GUERNEVILLE CA',
   'RUSSIAN R A JOHNSONS BEACH A GUERNEVILLE CA',
                 'RUSSIAN R A VACATION BEACH CA',
                    'BIG AUSTIN C A CAZADERO CA',
                       'AUSTIN C NR CAZADERO CA',
                  'RUSSIAN R A DUNCANS MILLS CA',
               'FREEZEOUT C NR DUNCANS MILLS CA',
                               '007N011W14NU01M',
                               '007N011W14NU03M',
                   'DUTCH BILL C A MONTE RIO CA',
  'RUSSIAN R A CASINI RANCH NR DUNCANS MILLS CA',
                      'RUSSIAN R A MONTE RIO CA',
                               '007N010W10H001M',
                  'AUSTIN C NR DUNCANS MILLS CA',
                               '007N010W07D001M',
                   'HULBERT C NR GUERNEVILLE CA',
                 'POCKET CYN C A GUERNEVILLE CA',
                               '008N009W31C002M',
                               '008N009W31C003M',
                               '008N009W31C004M',
                               '008N009W31C005M',
                       'FIFE C A GUERNEVILLE CA',
          'GREEN VALLEY C NR MIRABEL HEIGHTS CA',
   'RUSSIAN R A ODD FELLOWS PARK NR RIO NIDO CA',
                               '008N011W27N001M',
                               '008N010W28RU01M',
                       'HOBSON C NR HACIENDA CA',
                               '008N010W29H004M']
Length: 28, dtype: str

Selection by position

We can get data by position in the dataframe using the .iloc attribute

[12]:

info.iloc[0:2, 1:4]

[12]:

	site_no	station_nm	site_tp_cd
0	11467000	RUSSIAN R A HACIENDA BRIDGE NR GUERNEVILLE CA	ST
1	11467002	RUSSIAN R A JOHNSONS BEACH A GUERNEVILLE CA	ST

Selection by label

Pandas allows the user to get data from the dataframe by index and column labels

[13]:

info.loc[0:3, ["site_no", "station_nm", "site_tp_cd"]]

[13]:

	site_no	station_nm	site_tp_cd
0	11467000	RUSSIAN R A HACIENDA BRIDGE NR GUERNEVILLE CA	ST
1	11467002	RUSSIAN R A JOHNSONS BEACH A GUERNEVILLE CA	ST
2	11467006	RUSSIAN R A VACATION BEACH CA	ST
3	11467050	BIG AUSTIN C A CAZADERO CA	ST

Boolean indexing

pandas dataframes supports boolean indexing that allows a user to create a new dataframe with only the data that meets a boolean condition defined by the user.

Let’s get a dataframe of only groundwater sites from the info dataframe

[14]:

dfgw = info[info["site_tp_cd"] == "GW"]
dfgw

[14]:

	agency_cd	site_no	station_nm	site_tp_cd	lat_va	long_va	dec_lat_va	dec_long_va	coord_meth_cd	coord_acy_cd	...	local_time_fg	reliability_cd	gw_file_cd	nat_aqfr_cd	aqfr_cd	aqfr_type_cd	well_depth_va	hole_depth_va	depth_src_cd	project_no
7	USGS	382713123030401	007N011W14NU01M	GW	382712.5	1230303.5	38.453472	-123.050972	G	5	...	Y	C	YY Y	NaN	NaN	NaN	81.70	NaN	S	GGMC200
8	USGS	382713123030403	007N011W14NU03M	GW	382712.5	1230303.5	38.453472	-123.050972	G	5	...	Y	C	YY Y	NaN	NaN	NaN	32.56	NaN	S	GGMC200
12	USGS	382808122565401	007N010W10H001M	GW	382808.5	1225654.2	38.469028	-122.948389	G	5	...	Y	C	YY Y	NaN	NaN	NaN	22.00	22.0	D	00BHM8187
14	USGS	382819123010001	007N010W07D001M	GW	382819.9	1230100.8	38.472194	-123.016889	G	5	...	Y	C	YY	N100CACSTL	NaN	NaN	99.00	110.0	D	9677BHM32
17	USGS	383001122540701	008N009W31C002M	GW	383001.9	1225407.7	38.500528	-122.902139	G	5	...	Y	C	YY	N100CACSTL	NaN	NaN	80.00	80.0	D	9677BHM32
18	USGS	383003122540401	008N009W31C003M	GW	383003.3	1225404.4	38.500917	-122.901222	G	1	...	Y	C	YY Y	N100CACSTL	NaN	NaN	NaN	NaN	NaN	967760420
19	USGS	383003122540402	008N009W31C004M	GW	383003.3	1225404.4	38.500917	-122.901222	G	1	...	Y	C	Y	N100CACSTL	NaN	NaN	NaN	NaN	NaN	967760420
20	USGS	383003122540403	008N009W31C005M	GW	383003.3	1225404.4	38.500917	-122.901222	G	1	...	Y	C	YY Y	N100CACSTL	NaN	NaN	25.00	NaN	S	967760420
24	USGS	383016123041101	008N011W27N001M	GW	383016.3	1230411.0	38.504528	-123.069722	G	5	...	Y	C	YY Y	NaN	NaN	NaN	30.00	30.0	D	00BHM8187
25	USGS	383017122580301	008N010W28RU01M	GW	383017.4	1225802.5	38.504833	-122.967361	G	5	...	Y	C	YY	NaN	NaN	NaN	98.00	107.0	D	NaN
27	USGS	383034122590701	008N010W29H004M	GW	383034.4	1225907.9	38.509556	-122.985528	G	5	...	Y	C	YY Y	N100CACSTL	NaN	NaN	99.00	110.0	D	9677BHM32

11 rows × 42 columns

Reading and writing data to `.csv` files

Pandas has support to both read and write many types of files. For this example we are focusing on .csv files. For information on other file types that are supported see the ten minutes to pandas tutorial documentation

For this part we’ll write a new .csv file of the groundwater sites that we found in NWIS using to_csv().

to_csv() has a bunch of handy options for writing to file. For this example, I’m going to drop the index column while writing by passing index=False

[15]:

csv_file = data_path / "RussianRiverGWsites.csv"
dfgw.to_csv(csv_file, index=False)

Now we can load the csv file back into a pandas dataframe with the read_csv() method.

[16]:

dfgw2 = pd.read_csv(csv_file)
dfgw2

[16]:

	agency_cd	site_no	station_nm	site_tp_cd	lat_va	long_va	dec_lat_va	dec_long_va	coord_meth_cd	coord_acy_cd	...	local_time_fg	reliability_cd	gw_file_cd	nat_aqfr_cd	aqfr_cd	aqfr_type_cd	well_depth_va	hole_depth_va	depth_src_cd	project_no
0	USGS	382713123030401	007N011W14NU01M	GW	382712.5	1230303.5	38.453472	-123.050972	G	5	...	Y	C	YY Y	NaN	NaN	NaN	81.70	NaN	S	GGMC200
1	USGS	382713123030403	007N011W14NU03M	GW	382712.5	1230303.5	38.453472	-123.050972	G	5	...	Y	C	YY Y	NaN	NaN	NaN	32.56	NaN	S	GGMC200
2	USGS	382808122565401	007N010W10H001M	GW	382808.5	1225654.2	38.469028	-122.948389	G	5	...	Y	C	YY Y	NaN	NaN	NaN	22.00	22.0	D	00BHM8187
3	USGS	382819123010001	007N010W07D001M	GW	382819.9	1230100.8	38.472194	-123.016889	G	5	...	Y	C	YY	N100CACSTL	NaN	NaN	99.00	110.0	D	9677BHM32
4	USGS	383001122540701	008N009W31C002M	GW	383001.9	1225407.7	38.500528	-122.902139	G	5	...	Y	C	YY	N100CACSTL	NaN	NaN	80.00	80.0	D	9677BHM32
5	USGS	383003122540401	008N009W31C003M	GW	383003.3	1225404.4	38.500917	-122.901222	G	1	...	Y	C	YY Y	N100CACSTL	NaN	NaN	NaN	NaN	NaN	967760420
6	USGS	383003122540402	008N009W31C004M	GW	383003.3	1225404.4	38.500917	-122.901222	G	1	...	Y	C	Y	N100CACSTL	NaN	NaN	NaN	NaN	NaN	967760420
7	USGS	383003122540403	008N009W31C005M	GW	383003.3	1225404.4	38.500917	-122.901222	G	1	...	Y	C	YY Y	N100CACSTL	NaN	NaN	25.00	NaN	S	967760420
8	USGS	383016123041101	008N011W27N001M	GW	383016.3	1230411.0	38.504528	-123.069722	G	5	...	Y	C	YY Y	NaN	NaN	NaN	30.00	30.0	D	00BHM8187
9	USGS	383017122580301	008N010W28RU01M	GW	383017.4	1225802.5	38.504833	-122.967361	G	5	...	Y	C	YY	NaN	NaN	NaN	98.00	107.0	D	NaN
10	USGS	383034122590701	008N010W29H004M	GW	383034.4	1225907.9	38.509556	-122.985528	G	5	...	Y	C	YY Y	N100CACSTL	NaN	NaN	99.00	110.0	D	9677BHM32

11 rows × 42 columns

Class exercise 1

Using the methods presented in this notebook create a DataFrame of surface water sites from the info dataframe, write it to a csv file named "RussianRiverSWsites.csv", and read it back in as a new DataFrame

[17]:

csv_name = data_path / "RussianRiverSWsites.csv"
dfsw = info[info.site_tp_cd == "ST"]
dfsw.to_csv(csv_name, index=False)

dfsw = pd.read_csv(csv_name)
dfsw.head()

[17]:

	agency_cd	site_no	station_nm	site_tp_cd	lat_va	long_va	dec_lat_va	dec_long_va	coord_meth_cd	coord_acy_cd	...	local_time_fg	reliability_cd	gw_file_cd	nat_aqfr_cd	aqfr_cd	aqfr_type_cd	well_depth_va	hole_depth_va	depth_src_cd	project_no
0	USGS	11467000	RUSSIAN R A HACIENDA BRIDGE NR GUERNEVILLE CA	ST	383031.0	1225536.0	38.508482	-122.927734	M	F	...	Y	NaN	NNNNNNNN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
1	USGS	11467002	RUSSIAN R A JOHNSONS BEACH A GUERNEVILLE CA	ST	382958.0	1225950.0	38.499358	-122.998333	M	F	...	Y	NaN	NNNNNNNN	NaN	NaN	NaN	NaN	NaN	NaN	967760420.0
2	USGS	11467006	RUSSIAN R A VACATION BEACH CA	ST	382903.0	1230041.0	38.484080	-123.012500	M	F	...	Y	NaN	NNNNNNNN	NaN	NaN	NaN	NaN	NaN	NaN	967760420.0
3	USGS	11467050	BIG AUSTIN C A CAZADERO CA	ST	383215.0	1230518.0	38.537413	-123.089447	M	F	...	Y	NaN	NNNNNNNN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
4	USGS	11467200	AUSTIN C NR CAZADERO CA	ST	383024.0	1230407.0	38.506536	-123.069683	M	S	...	Y	NaN	NNNNNNNN	NaN	NaN	NaN	NaN	NaN	NaN	967700102.0

5 rows × 42 columns

Get timeseries data from NWIS for surface water sites

Now to start working with stream gage data from NWIS. We’re going to send all surface water sites to NWIS and get only sites with daily discharge measurements.

(11467002)

[18]:

# filter for only SW sites
dfsw = info[info.site_tp_cd == "ST"]

# create query
sites = dfsw.site_no.to_list()
pcode = "00060"
start_date = "1939-09-22"
end_date = "2023-12-31"
df, metadata = nwis.get_dv(
    sites=sites,
    start=start_date,
    end=end_date,
    parameterCd=pcode,
    multi_index=False
)
df.head()

[18]:

	site_no	00060_Mean	00060_Mean_cd
datetime
1939-10-01 00:00:00+00:00	11467000	185.0	A, e
1939-10-02 00:00:00+00:00	11467000	185.0	A, e
1939-10-03 00:00:00+00:00	11467000	185.0	A, e
1939-10-04 00:00:00+00:00	11467000	185.0	A, e
1939-10-05 00:00:00+00:00	11467000	185.0	A, e

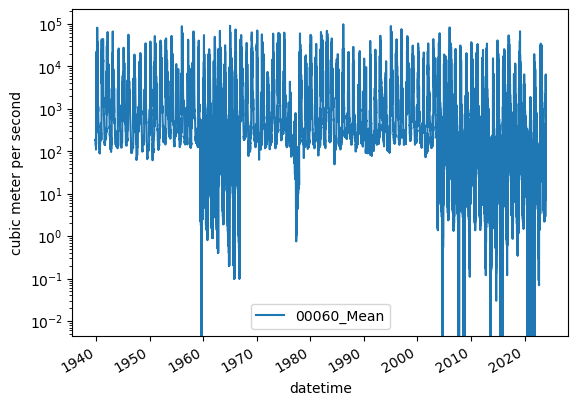
Awesome! There are two gages in this study area that have daily discharge data!

Inspect the data using `.plot()`

[19]:

ax = df.plot()
ax.set_ylabel(r"cubic meter per second")
ax.set_yscale("log")

../../../_images/notebooks_part0_python_intro_solutions_08_pandas_36_0.png

Updating column names

Let’s update column names for these gages based on their locations instead of their USGS gage id. First we’ll get name information from the info class and then we’ll use the station name information to remap the column names.

the rename() method accepts a dictionary that is formatted {current_col_name: new_col_name}

[20]:

df

[20]:

	site_no	00060_Mean	00060_Mean_cd
datetime
1939-10-01 00:00:00+00:00	11467000	185.0	A, e
1939-10-02 00:00:00+00:00	11467000	185.0	A, e
1939-10-03 00:00:00+00:00	11467000	185.0	A, e
1939-10-04 00:00:00+00:00	11467000	185.0	A, e
1939-10-05 00:00:00+00:00	11467000	185.0	A, e
...	...	...	...
2023-12-29 00:00:00+00:00	11467000	1970.0	A
2023-12-30 00:00:00+00:00	11467000	6170.0	A
2023-12-30 00:00:00+00:00	11467200	1390.0	A
2023-12-31 00:00:00+00:00	11467000	5970.0	A
2023-12-31 00:00:00+00:00	11467200	619.0	A

40848 rows × 3 columns

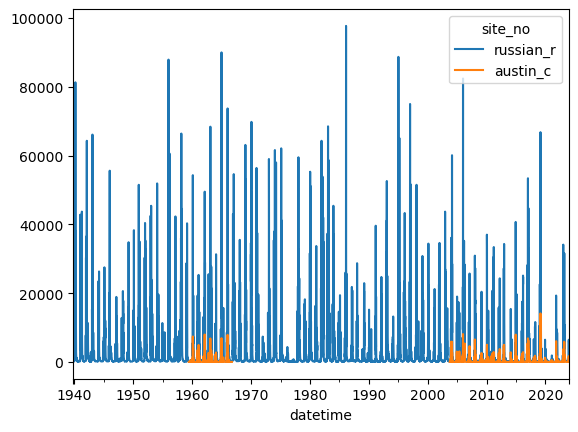
[21]:

df2 = df[['site_no', '00060_Mean']].pivot(columns=['site_no'])
df2.columns = df2.columns.get_level_values(1)

site_names = {site_no: '_'.join(name.split()[:2]).lower() for site_no, name
              in info.groupby('site_no')['station_nm'].first().loc[df2.columns].items()}
df2.rename(columns=site_names, inplace=True)
df2.plot()

[21]:

<Axes: xlabel='datetime'>

../../../_images/notebooks_part0_python_intro_solutions_08_pandas_39_1.png

Adding a new column of data to the dataframe

Adding new columns of data is relatively simple in pandas. The call signature is similar to a dictionary where df[“key”] = “some_array_of_values”

Let’s add a year column (water year) to the dataframe by getting the year from the index and adjusting it using np.where()

[22]:

df2['year'] = np.where(df2.index.month >=10, df2.index.year, df2.index.year - 1)

Manipulating data

Columns in a pandas dataframe can be manipulated similarly to working with a dictionary of numpy arrays. The discharge data units are $\frac{ft^3}{s}$, let’s accumulate this to daily discharge in $\frac {ft^3}{d}$.

The conversion for this is:

$ \frac{1 ft^3}{s} \times `:nbsphinx-math:frac{60s}{min}` \times `:nbsphinx-math:frac{60min}{hour}` \times `:nbsphinx-math:frac{24hours}{day}` \rightarrow `:nbsphinx-math:frac{ft^3}{day}` $

and then convert that to acre-feet (1 acre-ft = 43559.9)

[23]:

df2

[23]:

site_no	russian_r	austin_c	year
datetime
1939-10-01 00:00:00+00:00	185.0	NaN	1939
1939-10-02 00:00:00+00:00	185.0	NaN	1939
1939-10-03 00:00:00+00:00	185.0	NaN	1939
1939-10-04 00:00:00+00:00	185.0	NaN	1939
1939-10-05 00:00:00+00:00	185.0	NaN	1939
...	...	...	...
2023-12-27 00:00:00+00:00	888.0	965.0	2023
2023-12-28 00:00:00+00:00	1640.0	857.0	2023
2023-12-29 00:00:00+00:00	1970.0	1460.0	2023
2023-12-30 00:00:00+00:00	6170.0	1390.0	2023
2023-12-31 00:00:00+00:00	5970.0	619.0	2023

30773 rows × 3 columns

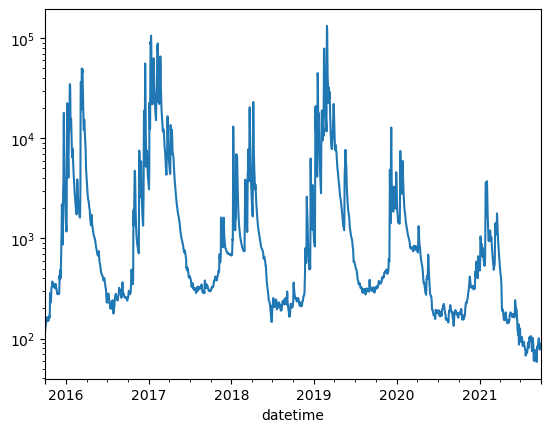
[24]:

conv = 60 * 60 * 24
df2["russian_r_cfd"] = df2.russian_r * conv
df2["russian_r_af"] = df2.russian_r_cfd / 43559.9
df2

# now let's plot up discharge from 2018 - 2020
dfplt = df2[(df2["year"] >= 2015) & (df2["year"] <= 2020)]
ax = dfplt["russian_r_af"].plot()
ax.set_yscale("log")

../../../_images/notebooks_part0_python_intro_solutions_08_pandas_44_0.png

Class exercise 2:

Using the methods described in the notebook. Convert the discharge for "austin_c" from $\frac{m^3}{s}$ acre-ft by adding two additional fields to df2 named "austin_c_cfs" and "austin_c_af".

After these two fields have been added to df2 use boolean indexing to create a new dataframe from 2015 through 2020. Finally plot the discharge data (in acre-ft) for “austin_cr”.

bonus exercise try to plot both "russian_r_af" and "austin_c_af" on the same plot

[25]:

conv = 60 * 60 * 24
df2["austin_c_cfd"] = df2.austin_c * conv
df2["austin_c_af"] = df2.austin_c_cfd / 43559.9
df2

# now let's plot up discharge from 2018 - 2020
dfplt = df2[(df2["year"] >= 2015) & (df2["year"] <= 2020)]
ax = dfplt["austin_c_af"].plot()
ax.set_yscale("log")

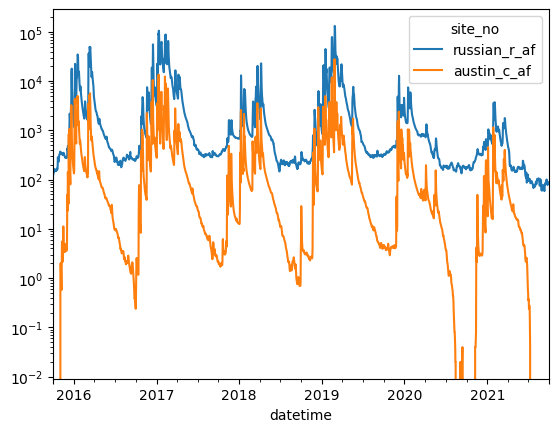
../../../_images/notebooks_part0_python_intro_solutions_08_pandas_46_0.png

[26]:

# now let's plot up discharge from 2018 - 2020
dfplt = df2[(df2["year"] >= 2015) & (df2["year"] <= 2020)]
ax = dfplt[["russian_r_af","austin_c_af"]].plot()
ax.set_yscale("log")

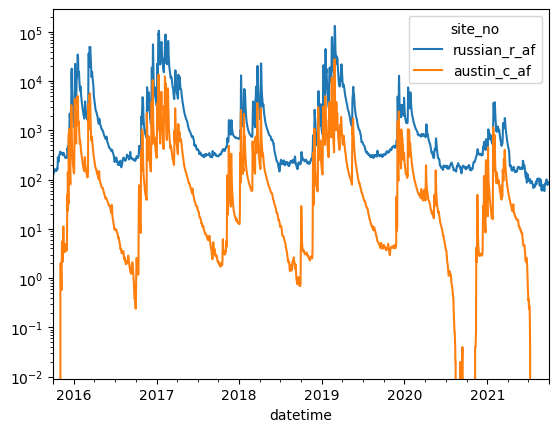
../../../_images/notebooks_part0_python_intro_solutions_08_pandas_47_0.png

groupby: grouping data and performing mathematical operations on it

groupby() is a powerful method that allows for performing statistical operations over a groups of “common” data within a dataframe.

For this example we’ll use it to get mean daily flows for the watershed. Pandas will group all common days of the year with each other and then calculate the mean value of these via the function .mean(). groupby() also supports other operations such as .median(), .sum(), max(), min(), std(), and other functions.

[27]:

df2["day_of_year"] = df2.index.day_of_year

df_mean_day = df2.groupby(by=["day_of_year"], as_index=False)[["russian_r_af", "austin_c_af"]].mean()
ax = df_mean_day[["russian_r_af", "austin_c_af"]].plot()
ax.set_yscale("log")

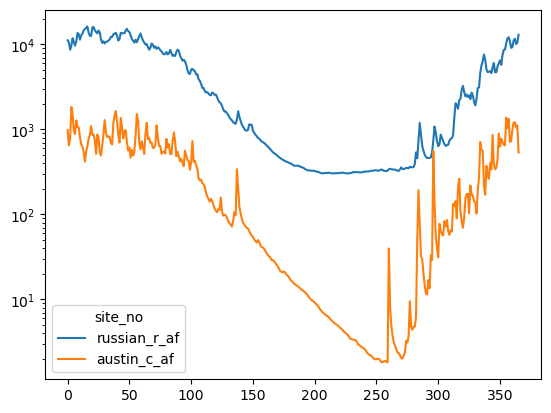
../../../_images/notebooks_part0_python_intro_solutions_08_pandas_49_0.png

We can see that around March flow starts decreasing heavily and doesn’t recover until sometime in october. What’s going on here? Let’s load some climate data and see what’s happening.

[28]:

cimis_file = data_path / "santa_rosa_CIMIS_83.csv"
df_cimis = pd.read_csv(cimis_file)
drop_list = ["qc"] + [f"qc.{i}" for i in range(1, 22)]
df_cimis.drop(columns=drop_list, inplace=True)
df_cimis

[28]:

	Stn Id	Stn Name	CIMIS Region	Date	Jul	ETo (in)	Precip (in)	Sol Rad (Ly/day)	Avg Vap Pres (mBars)	Max Air Temp (F)	...	Rose NNE	Rose ENE	Rose ESE	Rose SSE	Rose SSW	Rose WSW	Rose WNW	Rose NNW	Wind Run (miles)	Avg Soil Temp (F)
0	83	Santa Rosa	North Coast Valleys	1/1/1990	1	0.00	0.30	42.0	7.7	48.7	...	0.03	0.02	0.06	0.06	0.04	0.10	0.15	0.14	32.1	46.3
1	83	Santa Rosa	North Coast Valleys	1/2/1990	2	0.06	0.00	236.0	6.1	58.4	...	0.06	0.01	0.04	0.03	0.03	0.06	0.45	1.53	121.0	44.9
2	83	Santa Rosa	North Coast Valleys	1/3/1990	3	0.04	0.00	225.0	5.8	63.0	...	0.08	0.04	0.10	0.04	0.06	0.05	0.21	0.23	44.5	43.3
3	83	Santa Rosa	North Coast Valleys	1/4/1990	4	0.03	0.01	190.0	6.3	56.7	...	0.07	0.07	0.11	0.07	0.03	0.03	0.08	0.09	30.2	42.8
4	83	Santa Rosa	North Coast Valleys	1/5/1990	5	0.04	0.00	192.0	7.2	59.1	...	0.08	0.13	0.33	0.08	0.04	0.08	0.07	0.05	45.2	43.7
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
11948	83	Santa Rosa	North Coast Valleys	9/18/2022	261	0.03	0.77	113.0	16.4	66.8	...	0.01	0.04	0.29	0.51	0.14	0.01	0.00	0.00	197.4	65.2
11949	83	Santa Rosa	North Coast Valleys	9/19/2022	262	0.14	0.02	424.0	15.6	73.9	...	0.09	0.07	0.08	0.17	0.09	0.28	0.15	0.07	108.9	65.9
11950	83	Santa Rosa	North Coast Valleys	9/20/2022	263	0.10	0.00	330.0	13.9	72.6	...	0.08	0.04	0.10	0.11	0.18	0.25	0.15	0.10	79.6	65.8
11951	83	Santa Rosa	North Coast Valleys	9/21/2022	264	0.15	0.07	458.0	14.8	75.5	...	0.09	0.05	0.13	0.16	0.18	0.22	0.08	0.09	103.3	66.7
11952	83	Santa Rosa	North Coast Valleys	9/22/2022	265	0.17	0.00	494.0	13.1	82.9	...	0.14	0.06	0.09	0.10	0.11	0.20	0.12	0.19	83.7	66.3

11953 rows × 27 columns

[29]:

df_mean_clim = df_cimis.groupby(by=["Jul"], as_index=False)[["ETo (in)", "Precip (in)"]].mean()
df_mean_clim = df_mean_clim.rename(columns={"Jul": "day_of_year"})
df_mean_clim.head()

[29]:

	day_of_year	ETo (in)	Precip (in)
0	1	0.031212	0.335455
1	2	0.031212	0.155152
2	3	0.030303	0.195484
3	4	0.030909	0.190303
4	5	0.034242	0.150000

Joining two `DataFrames` with an inner join

Inner joins can be made in pandas with the merge() method. As inner join, joins two dataframes on a common key or values, when a key or value exists in one dataframe, but not the other that row of data will be excluded from the joined dataframe.

There are a number of other ways to join dataframes in pandas. Detailed examples and discussion of the different merging methods can be found here

[30]:

df_merged = pd.merge(df_mean_day, df_mean_clim, on=["day_of_year",])
df_merged.head()

[30]:

	day_of_year	russian_r_af	austin_c_af	ETo (in)	Precip (in)
0	1	11169.447129	982.247985	0.031212	0.335455
1	2	10601.346651	648.518661	0.031212	0.155152
2	3	8662.758966	777.478369	0.030303	0.195484
3	4	9604.154280	1831.494379	0.030909	0.190303
4	5	11811.951556	1508.267191	0.034242	0.150000

[31]:

cols = [i for i in list(df_merged) if i != "day_of_year"]
ax = df_merged[cols].plot()
ax.set_yscale("log")

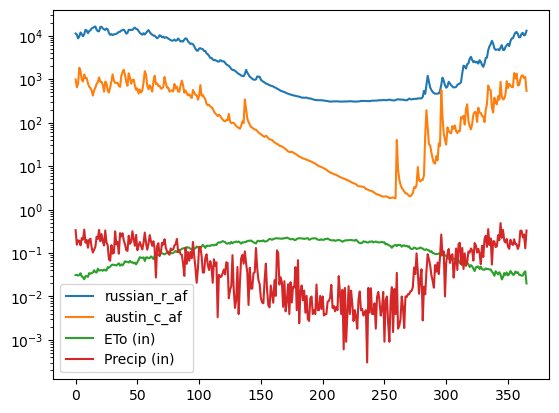
../../../_images/notebooks_part0_python_intro_solutions_08_pandas_55_0.png

This starts to make a little more sense! We can see that this area gets most of it’s precipitation in the winter and early spring. The evapotranspiration curve shows what we’d expect: that there is more evapotranspiration in the summer than the winter.

Stepping back for a minute: exploring Merge and Concat

Merge and concat are very powerful and important methods for combining pandas DataFrames (and later geopandas GeoDataFrames). This section takes a moment, as an aside to explore some of the common funtions and options for performing merges and concatenation.

The `merge` method

Pandas merge method allows the user to join two dataframes based on column values. There are a few methods that can be used to control the type of merge and the result.

inner: operates as a intersection of the data and keeps rows from both dataframes if the row has a matching key in both dataframes.
outer: operates as a union and joins all rows from both dataframes, fills columns with nan where data is not available for a row.
left: keeps all rows from the ‘left’ dataframe and joins columns from the right
right: keeps all rows from the ‘right’ dataframe and joins columns from the left

[32]:

ex0 = {
    "name": [],
    "childhood_dream_job": []
}
ex1 = {
    "name": [],
    "age": []
}

[ ]:

[ ]:

[ ]:

The `concat` method

Pandas concat method allows the user to concatenate dataframes together

[33]:

gw = info[info.site_tp_cd == "GW"]
sw = info[info.site_tp_cd == "ST"]
sw = sw[list(sw)[0:8]]
sw.head()

[33]:

	agency_cd	site_no	station_nm	site_tp_cd	lat_va	long_va	dec_lat_va	dec_long_va
0	USGS	11467000	RUSSIAN R A HACIENDA BRIDGE NR GUERNEVILLE CA	ST	383031.0	1225536.0	38.508482	-122.927734
1	USGS	11467002	RUSSIAN R A JOHNSONS BEACH A GUERNEVILLE CA	ST	382958.0	1225950.0	38.499358	-122.998333
2	USGS	11467006	RUSSIAN R A VACATION BEACH CA	ST	382903.0	1230041.0	38.484080	-123.012500
3	USGS	11467050	BIG AUSTIN C A CAZADERO CA	ST	383215.0	1230518.0	38.537413	-123.089447
4	USGS	11467200	AUSTIN C NR CAZADERO CA	ST	383024.0	1230407.0	38.506536	-123.069683

[34]:

newdf = pd.concat((gw, sw), ignore_index=True)
newdf

[34]:

	agency_cd	site_no	station_nm	site_tp_cd	lat_va	long_va	dec_lat_va	dec_long_va	coord_meth_cd	coord_acy_cd	...	local_time_fg	reliability_cd	gw_file_cd	nat_aqfr_cd	aqfr_cd	aqfr_type_cd	well_depth_va	hole_depth_va	depth_src_cd	project_no
0	USGS	382713123030401	007N011W14NU01M	GW	382712.5	1230303.5	38.453472	-123.050972	G	5	...	Y	C	YY Y	NaN	NaN	NaN	81.70	NaN	S	GGMC200
1	USGS	382713123030403	007N011W14NU03M	GW	382712.5	1230303.5	38.453472	-123.050972	G	5	...	Y	C	YY Y	NaN	NaN	NaN	32.56	NaN	S	GGMC200
2	USGS	382808122565401	007N010W10H001M	GW	382808.5	1225654.2	38.469028	-122.948389	G	5	...	Y	C	YY Y	NaN	NaN	NaN	22.00	22.0	D	00BHM8187
3	USGS	382819123010001	007N010W07D001M	GW	382819.9	1230100.8	38.472194	-123.016889	G	5	...	Y	C	YY	N100CACSTL	NaN	NaN	99.00	110.0	D	9677BHM32
4	USGS	383001122540701	008N009W31C002M	GW	383001.9	1225407.7	38.500528	-122.902139	G	5	...	Y	C	YY	N100CACSTL	NaN	NaN	80.00	80.0	D	9677BHM32
5	USGS	383003122540401	008N009W31C003M	GW	383003.3	1225404.4	38.500917	-122.901222	G	1	...	Y	C	YY Y	N100CACSTL	NaN	NaN	NaN	NaN	NaN	967760420
6	USGS	383003122540402	008N009W31C004M	GW	383003.3	1225404.4	38.500917	-122.901222	G	1	...	Y	C	Y	N100CACSTL	NaN	NaN	NaN	NaN	NaN	967760420
7	USGS	383003122540403	008N009W31C005M	GW	383003.3	1225404.4	38.500917	-122.901222	G	1	...	Y	C	YY Y	N100CACSTL	NaN	NaN	25.00	NaN	S	967760420
8	USGS	383016123041101	008N011W27N001M	GW	383016.3	1230411.0	38.504528	-123.069722	G	5	...	Y	C	YY Y	NaN	NaN	NaN	30.00	30.0	D	00BHM8187
9	USGS	383017122580301	008N010W28RU01M	GW	383017.4	1225802.5	38.504833	-122.967361	G	5	...	Y	C	YY	NaN	NaN	NaN	98.00	107.0	D	NaN
10	USGS	383034122590701	008N010W29H004M	GW	383034.4	1225907.9	38.509556	-122.985528	G	5	...	Y	C	YY Y	N100CACSTL	NaN	NaN	99.00	110.0	D	9677BHM32
11	USGS	11467000	RUSSIAN R A HACIENDA BRIDGE NR GUERNEVILLE CA	ST	383031.0	1225536.0	38.508482	-122.927734	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
12	USGS	11467002	RUSSIAN R A JOHNSONS BEACH A GUERNEVILLE CA	ST	382958.0	1225950.0	38.499358	-122.998333	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
13	USGS	11467006	RUSSIAN R A VACATION BEACH CA	ST	382903.0	1230041.0	38.484080	-123.012500	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
14	USGS	11467050	BIG AUSTIN C A CAZADERO CA	ST	383215.0	1230518.0	38.537413	-123.089447	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
15	USGS	11467200	AUSTIN C NR CAZADERO CA	ST	383024.0	1230407.0	38.506536	-123.069683	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
16	USGS	11467210	RUSSIAN R A DUNCANS MILLS CA	ST	382713.0	1230254.0	38.453525	-123.049446	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
17	USGS	382701123025801	FREEZEOUT C NR DUNCANS MILLS CA	ST	382701.0	1230258.0	38.450278	-123.049444	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
18	USGS	382752123003401	DUTCH BILL C A MONTE RIO CA	ST	382752.0	1230034.0	38.464444	-123.009444	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
19	USGS	382754123030501	RUSSIAN R A CASINI RANCH NR DUNCANS MILLS CA	ST	382754.0	1230305.0	38.465000	-123.051389	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
20	USGS	382757123003801	RUSSIAN R A MONTE RIO CA	ST	382757.0	1230038.0	38.465833	-123.010556	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
21	USGS	382815123024601	AUSTIN C NR DUNCANS MILLS CA	ST	382815.0	1230246.0	38.470833	-123.046111	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
22	USGS	382944123002901	HULBERT C NR GUERNEVILLE CA	ST	382944.0	1230029.0	38.495556	-123.008056	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
23	USGS	382955122594101	POCKET CYN C A GUERNEVILLE CA	ST	382955.0	1225941.0	38.498611	-122.994722	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
24	USGS	383006123000601	FIFE C A GUERNEVILLE CA	ST	383006.0	1230006.0	38.501667	-123.001667	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
25	USGS	383009122543001	GREEN VALLEY C NR MIRABEL HEIGHTS CA	ST	383009.0	1225430.0	38.502500	-122.908333	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
26	USGS	383012122574501	RUSSIAN R A ODD FELLOWS PARK NR RIO NIDO CA	ST	383012.0	1225745.0	38.503333	-122.962500	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
27	USGS	383028122554501	HOBSON C NR HACIENDA CA	ST	383028.0	1225545.0	38.507778	-122.929167	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN

28 rows × 42 columns

Back to working with our climate and stream data

Is there anything else we can look at that might give us more insights into this basin?

Let’s try looking at long term, yearly trends to see what’s there.

[35]:

year = []
for dstr in df_cimis.Date.values:
    mo, d, yr = [int(i) for i in dstr.split("/")]
    if mo < 10:
        year.append(yr - 1)
    else:
        year.append(yr)
df_cimis["year"] = year
df_cimis.head()

[35]:

	Stn Id	Stn Name	CIMIS Region	Date	Jul	ETo (in)	Precip (in)	Sol Rad (Ly/day)	Avg Vap Pres (mBars)	Max Air Temp (F)	...	Rose ENE	Rose ESE	Rose SSE	Rose SSW	Rose WSW	Rose WNW	Rose NNW	Wind Run (miles)	Avg Soil Temp (F)	year
0	83	Santa Rosa	North Coast Valleys	1/1/1990	1	0.00	0.30	42.0	7.7	48.7	...	0.02	0.06	0.06	0.04	0.10	0.15	0.14	32.1	46.3	1989
1	83	Santa Rosa	North Coast Valleys	1/2/1990	2	0.06	0.00	236.0	6.1	58.4	...	0.01	0.04	0.03	0.03	0.06	0.45	1.53	121.0	44.9	1989
2	83	Santa Rosa	North Coast Valleys	1/3/1990	3	0.04	0.00	225.0	5.8	63.0	...	0.04	0.10	0.04	0.06	0.05	0.21	0.23	44.5	43.3	1989
3	83	Santa Rosa	North Coast Valleys	1/4/1990	4	0.03	0.01	190.0	6.3	56.7	...	0.07	0.11	0.07	0.03	0.03	0.08	0.09	30.2	42.8	1989
4	83	Santa Rosa	North Coast Valleys	1/5/1990	5	0.04	0.00	192.0	7.2	59.1	...	0.13	0.33	0.08	0.04	0.08	0.07	0.05	45.2	43.7	1989

5 rows × 28 columns

[36]:

df2.head()

[36]:

site_no	russian_r	austin_c	year	russian_r_cfd	russian_r_af	austin_c_cfd	austin_c_af	day_of_year
datetime
1939-10-01 00:00:00+00:00	185.0	NaN	1939	15984000.0	366.942991	NaN	NaN	274
1939-10-02 00:00:00+00:00	185.0	NaN	1939	15984000.0	366.942991	NaN	NaN	275
1939-10-03 00:00:00+00:00	185.0	NaN	1939	15984000.0	366.942991	NaN	NaN	276
1939-10-04 00:00:00+00:00	185.0	NaN	1939	15984000.0	366.942991	NaN	NaN	277
1939-10-05 00:00:00+00:00	185.0	NaN	1939	15984000.0	366.942991	NaN	NaN	278

`.aggregate()`

The pandas .aggregate() can be used with .groupy() to perform multiple statistical operations.

Example usage could be:

agdf = df2.groupby(by=["day_of_year"], as_index=False)["austin_c_af"].aggregate([np.min, np.max, np.mean, np.std])

And would return a dataframe grouped by the day of year and take the min, max, mean, and standard deviation of these data.

Class exercise 3: groupy, aggregate, and merge

For this exercise we need to produce yearly mean and standard deviation flows for the russian_r_af variable and merge the data with yearly mean precipitation and evapotranspiration

Hints:

df2 and df_cimis are the dataframes these operations should be performed on
use .groupby() to group by the year and do precip and ETo in separate groupby routines
rename the columns in the ETo aggregated dataframe and the Precip dataframe to mean_et, std_et, mean_precip, std_precip
np.mean and np.std can be used to calculate mean and std flows

Name your final joined dataframe df_yearly

[37]:

dfg0 = df2.groupby(by=["year"], as_index=False)["russian_r_af"].aggregate(['mean', 'std'])
dfg1 = df_cimis.groupby(by=["year"], as_index=False)["ETo (in)"].aggregate(['mean', 'std'])
dfg2 = df_cimis.groupby(by=["year"], as_index=False)["Precip (in)"].aggregate(['mean', 'std'])

dfm1 = pd.merge(dfg0, dfg1, on=["year"], suffixes=(None, "_et"))
df_yearly = pd.merge(dfm1, dfg2, on=["year"], suffixes=(None, "_precip"))

df_yearly

[37]:

	year	mean	std	mean_et	std_et	mean_precip	std_precip
0	1989	1388.134060	2703.398315	0.160513	0.080539	0.067473	0.284019
1	1990	2105.130611	7210.539138	0.113671	0.067419	0.081642	0.353434
2	1991	2180.262423	5581.173315	0.117268	0.067521	0.086940	0.233645
3	1992	5746.248446	11726.314669	0.122712	0.077676	0.128329	0.312310
4	1993	1528.091360	3052.871464	0.121781	0.073195	0.060168	0.225893
5	1994	9581.534959	22426.346294	0.113178	0.076706	0.151479	0.433991
6	1995	5575.848053	10440.114353	0.122814	0.078691	0.112596	0.416613
7	1996	5600.840663	16501.510310	0.129699	0.077105	0.102959	0.348520
8	1997	8587.944090	16139.648496	0.111589	0.075997	0.153068	0.383740
9	1998	4271.672888	7810.405143	0.123479	0.077184	0.086986	0.287404
10	1999	3510.811474	7712.677405	0.120546	0.074941	0.073425	0.254732
11	2000	1736.410643	4474.354276	0.127562	0.077590	0.058658	0.180318
12	2001	3625.296220	7794.142971	0.124712	0.077907	0.111044	0.355845
13	2002	5257.492880	10816.766181	0.123096	0.074760	0.103205	0.394435
14	2003	4723.322590	11718.629659	0.130546	0.078522	0.081995	0.327512
15	2004	3989.109667	6020.134120	0.117068	0.073038	0.095945	0.292390
16	2005	9004.490274	17931.497470	0.116658	0.073711	0.123123	0.384322
17	2006	1775.969842	4655.125526	0.123890	0.073490	0.056947	0.204511
18	2007	2696.274988	7169.983326	0.127377	0.076249	0.066066	0.270427
19	2008	1591.079482	4437.148385	0.119425	0.071221	0.052795	0.195192
20	2009	3869.030053	8304.931111	0.108219	0.070222	0.096411	0.308841
21	2010	5179.675425	9723.981660	0.114192	0.073108	0.101616	0.276342
22	2011	1877.259966	4587.983835	0.123962	0.071181	0.061233	0.278723
23	2012	2669.014799	7632.740020	0.122164	0.071272	0.066904	0.263863
24	2013	1062.237059	2976.193603	0.128849	0.068012	0.050740	0.297342
25	2014	2086.730478	6661.336955	0.128274	0.071913	0.061507	0.270112
26	2015	3395.358018	7587.288287	0.106011	0.059232	0.065495	0.233080
27	2016	8686.857030	16763.980172	0.119699	0.077931	0.108027	0.329238
28	2017	1443.417058	2746.964668	0.128055	0.075172	0.061616	0.272836
29	2018	6129.493976	14070.439880	0.130301	0.079187	0.115014	0.385471
30	2019	928.754876	1323.893808	0.137896	0.078000	0.039016	0.148017
31	2020	410.464250	515.126426	0.140959	0.073783	0.032027	0.126727
32	2021	1435.621183	3601.895852	0.134090	0.077279	0.078627	0.411521

Lets examine the long term flow record for the Russian River

[38]:

df_y_flow = df2.groupby(by=["year"], as_index=False)["russian_r_af"].aggregate(['mean', 'std'])

fig = plt.figure(figsize=(12,4))

lower_ci = df_y_flow["mean"] - 2 * df_y_flow['std']
lower_ci = np.where(lower_ci < 0, 0, lower_ci)
upper_ci = df_y_flow["mean"] + 2 * df_y_flow['std']
ax = df_y_flow["mean"].plot(style="b.-")
ax.fill_between(df_y_flow.index, lower_ci, upper_ci, color="b", alpha=0.5);

../../../_images/notebooks_part0_python_intro_solutions_08_pandas_74_0.png

From this plot it looks like the long term trend in yearly discharge in the Russian River has been decreasing. We will revisit and test this later.

First let’s see if there are any relationships between yearly discharge and climate

[39]:

dfg0 = df2.groupby(by=["year"], as_index=False)["russian_r_af"].aggregate(['mean', 'std', 'sum'])
dfg1 = df_cimis.groupby(by=["year"], as_index=False)["ETo (in)"].aggregate(['mean', 'std', 'sum'])
dfg2 = df_cimis.groupby(by=["year"], as_index=False)["Precip (in)"].aggregate(['mean', 'std', 'sum'])
dfm1 = pd.merge(dfg0, dfg1, on=["year"], suffixes=(None, "_et"))
df_yearly = pd.merge(dfm1, dfg2, on=["year"], suffixes=(None, "_precip"))

fig = plt.figure(figsize=(12,4))

lower_ci = df_yearly["mean"] - 2 * df_yearly['std']
lower_ci = np.where(lower_ci < 0, 0, lower_ci)
upper_ci = df_yearly["mean"] + 2 * df_yearly['std']
ax = df_yearly["mean"].plot(style="b.-", label="flow_af")
ax.fill_between(df_yearly.index, lower_ci, upper_ci, color="b", alpha=0.5)
ax2 = ax.twinx()
ax2.plot(df_yearly.index, df_yearly.sum_precip, "k--", lw=1.5, label="Precip")
ax2.plot(df_yearly.index, df_yearly.sum_et, "r.--", lw=1.5, label="ET")
plt.legend()
plt.show();

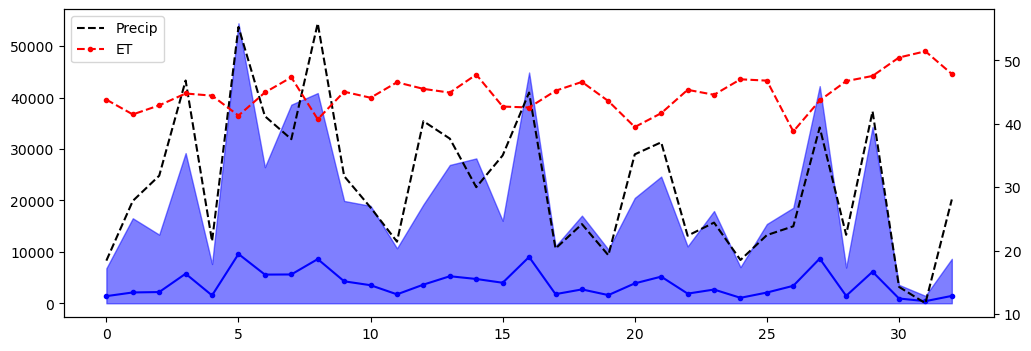
../../../_images/notebooks_part0_python_intro_solutions_08_pandas_76_0.png

As expected, precipitation amount is the main driver of the yearly discharge regime here

Baseflow separation

Baseflow separation is a method to separate the quick response hydrograph (storm runoff) from the long term flow. We’re going to go back to the complete daily dataset to perform this operation. The following cell contains a low pass filtration method that is used for digital baseflow separation. We’ll use these in our analysis

[40]:

def _baseflow_low_pass_filter(arr, beta, enforce):
    """
    Private method to apply digital baseflow separation filter
    (Lyne & Hollick, 1979; Nathan & Mcmahon, 1990;
    Boughton, 1993; Chapman & Maxwell, 1996).

    This method should not be called by the user!

    Method removes "spikes" which would be consistent with storm flow
    events from data.

    Parameters
    ----------
    arr : np.array
        streamflow or municipal pumping time series

    beta : float
        baseflow filtering parameter that ranges from 0 - 1
        values in 0.8 - 0.95 range used in literature for
        streamflow baseflow separation

    enforce : bool
        enforce physical constraint of baseflow less than measured flow

    Returns
    -------
        np.array of filtered data
    """
    # prepend 10 records to data for initial spin up
    # these records will be dropped before returning data to user
    qt = np.zeros((arr.size + 10,), dtype=float)
    qt[0:10] = arr[0:10]
    qt[10:] = arr[:]

    qdt = np.zeros((arr.size + 10,), dtype=float)
    qbf = np.zeros((arr.size + 10,), dtype=float)

    y = (1. + beta) / 2.

    for ix in range(qdt.size):
        if ix == 0:
            qbf[ix] = qt[ix]
            continue

        x = beta * qdt[ix - 1]
        z = qt[ix] - qt[ix - 1]
        qdt[ix] = x + (y * z)

        qb = qt[ix] - qdt[ix]
        if enforce:
            if qb > qt[ix]:
                qbf[ix] = qt[ix]
            else:
                qbf[ix] = qb

        else:
            qbf[ix] = qb

    return qbf[10:]


def baseflow_low_pass_filter(arr, beta=0.9, T=1, enforce=True):
    """
    User method to apply digital baseflow separation filter
    (Lyne & Hollick, 1979; Nathan & Mcmahon, 1990;
    Boughton, 1993; Chapman & Maxwell, 1996).

    Method removes "spikes" which would be consistent with storm flow
    events from data.

    Parameters
    ----------
    arr : np.array
        streamflow or municipal pumping time series

    beta : float
        baseflow filtering parameter that ranges from 0 - 1
        values in 0.8 - 0.95 range used in literature for
        streamflow baseflow separation

    T : int
        number of recursive filtering passes to apply to the data

    enforce : bool
        enforce physical constraint of baseflow less than measured flow

    Returns
    -------
        np.array of baseflow
    """
    for _ in range(T):
        arr = _baseflow_low_pass_filter(arr, beta, enforce)

    return arr

Class exercise 4: baseflow separation

Using the full dataframe discharge dataframe, df2, get the baseflows for the Russian River (in acre-ft) and add these to the dataframe as a new column named russian_bf_af.

The function baseflow_low_pass_filter() will be used to perform baseflow. This function takes a numpy array of stream discharge and runs a digital low pass filtration method to calculate baseflow.

After performing baseflow separation plot both the baseflow and the total discharge for the years 2015 - 2017.

Hints:

make sure to use the .values property when you get discharge data from the pandas dataframe
feel free to play with the input parameters beta and T.
- beta is commonly between 0.8 - 0.95 for hydrologic problems.
- T is the number of filter passes over the data, therefore increasing T will create a smoother profile. I recommend starting with a T value of around 5 and adjusting it to see how it changes the baseflow profile.

[41]:

baseflow = baseflow_low_pass_filter(df2["russian_r_af"].values, beta=0.90, T=5)
df2["russian_bf_af"] = baseflow

fig = plt.figure(figsize=(15, 10))
tdf = df2[(df2.year >= 2015) & (df2.year <= 2017)]
ax = tdf[["russian_r_af", "russian_bf_af"]].plot()
ax.set_yscale("log");

<Figure size 1500x1000 with 0 Axes>

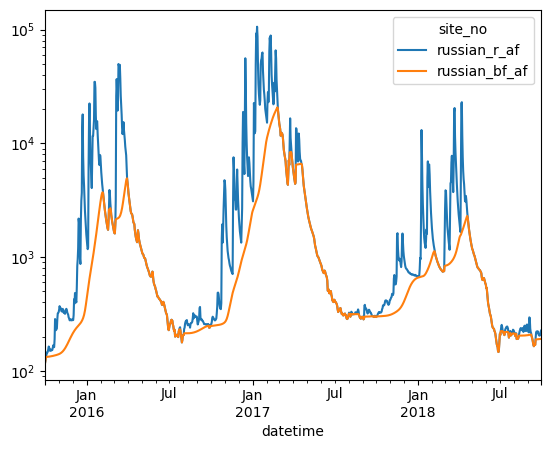
../../../_images/notebooks_part0_python_intro_solutions_08_pandas_81_1.png

Looking at trends and seasonal cycles in the data with `statsmodels`

statsmodels is a Python module that provides classes and functions for the estimation of many different statistical models, as well as for conducting statistical tests, and statistical data exploration. For more information on statsmodels and it’s many features visit the getting started guide

For this example we’ll be using time series analysis to perform a seasonal decomposition using moving averages. The statsmodels function seasonal_decompose will perform this analysis and return the data trend, seasonal fluctuations, and residuals.

[42]:

df2["russian_bf_af"] = baseflow_low_pass_filter(df2["russian_r_af"].values, beta=0.9, T=5)
# drop nan values prior to running decomposition
dfsm = df2[df2['russian_bf_af'].notna()]

dfsm.head()
# decompose
decomposition = sm.tsa.seasonal_decompose(dfsm["russian_bf_af"], period=365, model="additive")

decomposition.plot()
mpl.rcParams['figure.figsize'] = [14, 14];

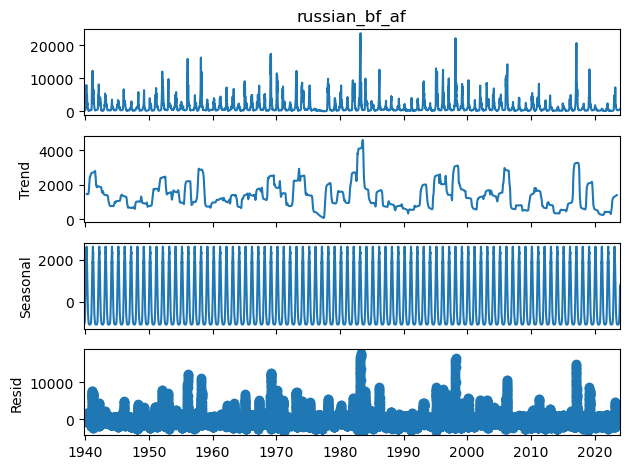
../../../_images/notebooks_part0_python_intro_solutions_08_pandas_83_0.png

Now let’s plot our baseflow trend against the baseflow we calculated

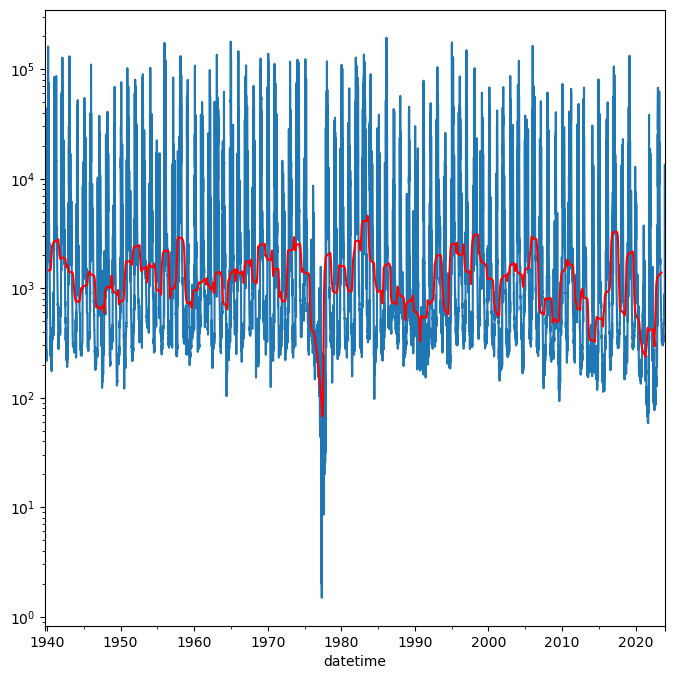
[43]:

fig, ax = plt.subplots(figsize=(8, 8))

ax = df2["russian_r_af"].plot(ax=ax)
ax.plot(decomposition.trend.index, decomposition.trend, "r-", lw=1.5)
ax.set_yscale('log')
plt.savefig("russian_river.png")

/tmp/ipykernel_10068/1871956059.py:4: UserWarning: This axis already has a converter set and is updating to a potentially incompatible converter
  ax.plot(decomposition.trend.index, decomposition.trend, "r-", lw=1.5)

../../../_images/notebooks_part0_python_intro_solutions_08_pandas_85_1.png

What’s going on at the end of the 1970’s? Why is the baseflow trend so low and peak flows are also low?

From “California’s Most Significant Droughts”, Chapter 3

The setting for the 1976-77 drought differed significantly from the dry times of the 1920s-30s. Although only a two-year event, its hydrology was severe. Based on 114 years of computed statewide runoff, 1977 occupies rank 114 (driest year) and 1976 is in rank 104. The drought was notable for the impacts experienced by water agencies that were unprepared for such conditions. One reason for the lack of preparedness was the perception of relatively ample water supplies in most areas of the state.

We can also see the analysis that there is an overall reduction in baseflow from 1940’s to the 2020’s

Writing yearly plots of data to a PDF document

We can write the plots we make with pandas to a multipage pdf using matplotlib’s PdfPages. For this example we’ll make yearly plots of all of the discharge, baseflow, and baseflow trend and bundle them into a single pdf document.

[44]:

# add the decomposition trend to the dataframe to make plotting easy
df2["baseflow_trend"] = decomposition.trend

pdf_file = data_path / "all_years_russian.pdf"
with PdfPages(pdf_file) as outpdf:
    for year in sorted(df2.year.unique()):
        plt.figure()
        tdf = df2[df2.year == year]
        tdf[["russian_r_af", "russian_bf_af", "baseflow_trend"]].plot()
        plt.xlabel("date")
        plt.ylabel("acre-feet")
        plt.ylim([1, 300000])
        plt.yscale("log")
        plt.tight_layout()
        outpdf.savefig()
        plt.close('all')

Go into the “data/pandas” and open up the file “all_years_russian.pdf” to check out the plots.

Back to the basics:

Now that we’ve done some analysis on real data, let’s go back to the basic and briefly discuss how to adjust data values in pandas

Adjusting a whole column of data values

Because pandas series objects (columns) are built off of numpy, we can perform mathematical operations in place on a whole column similarly to numpy arrays

[45]:

df3 = df2.copy()
# Adding values
df3["russian_r"] += 10000

# Subtracting values
df3["russian_r"] -= 10000

# multiplication
df3["russian_r"] *= 5

# division
df3["russian_r"] /= 5

# more complex operations
df3["russian_r"] = np.log10(df3["russian_r"].values)
df3.head()

[45]:

site_no	russian_r	austin_c	year	russian_r_cfd	russian_r_af	austin_c_cfd	austin_c_af	day_of_year	russian_bf_af	baseflow_trend
datetime
1939-10-01 00:00:00+00:00	2.267172	NaN	1939	15984000.0	366.942991	NaN	NaN	274	366.942991	NaN
1939-10-02 00:00:00+00:00	2.267172	NaN	1939	15984000.0	366.942991	NaN	NaN	275	366.942991	NaN
1939-10-03 00:00:00+00:00	2.267172	NaN	1939	15984000.0	366.942991	NaN	NaN	276	366.942991	NaN
1939-10-04 00:00:00+00:00	2.267172	NaN	1939	15984000.0	366.942991	NaN	NaN	277	366.942991	NaN
1939-10-05 00:00:00+00:00	2.267172	NaN	1939	15984000.0	366.942991	NaN	NaN	278	366.942991	NaN

updating values by position

We can update single or multiple values by their position in the dataframe using .iloc

[46]:

df3.iloc[0, 1] = 999
df3.head()

[46]:

site_no	russian_r	austin_c	year	russian_r_cfd	russian_r_af	austin_c_cfd	austin_c_af	day_of_year	russian_bf_af	baseflow_trend
datetime
1939-10-01 00:00:00+00:00	2.267172	999.0	1939	15984000.0	366.942991	NaN	NaN	274	366.942991	NaN
1939-10-02 00:00:00+00:00	2.267172	NaN	1939	15984000.0	366.942991	NaN	NaN	275	366.942991	NaN
1939-10-03 00:00:00+00:00	2.267172	NaN	1939	15984000.0	366.942991	NaN	NaN	276	366.942991	NaN
1939-10-04 00:00:00+00:00	2.267172	NaN	1939	15984000.0	366.942991	NaN	NaN	277	366.942991	NaN
1939-10-05 00:00:00+00:00	2.267172	NaN	1939	15984000.0	366.942991	NaN	NaN	278	366.942991	NaN

updating values based on location

We can update values in the dataframe based on their index and column headers too using .loc

[47]:

df3.loc[df3.index[0], 'russian_r'] *= 100
df3.head()

[47]:

site_no	russian_r	austin_c	year	russian_r_cfd	russian_r_af	austin_c_cfd	austin_c_af	day_of_year	russian_bf_af	baseflow_trend
datetime
1939-10-01 00:00:00+00:00	226.717173	999.0	1939	15984000.0	366.942991	NaN	NaN	274	366.942991	NaN
1939-10-02 00:00:00+00:00	2.267172	NaN	1939	15984000.0	366.942991	NaN	NaN	275	366.942991	NaN
1939-10-03 00:00:00+00:00	2.267172	NaN	1939	15984000.0	366.942991	NaN	NaN	276	366.942991	NaN
1939-10-04 00:00:00+00:00	2.267172	NaN	1939	15984000.0	366.942991	NaN	NaN	277	366.942991	NaN
1939-10-05 00:00:00+00:00	2.267172	NaN	1939	15984000.0	366.942991	NaN	NaN	278	366.942991	NaN

Class exercise 5: setting data

The russian river discharge in cubic feet per day highly variable and represented by large numbers. To make this data easier to read and plot, update it to a log10 representation.

Then use either a location based method to change the value in austin_c on 10-4-1939 to 0.

Finally display the first 5 records in the notebook.

[48]:

df3["russian_r_cfd"] = np.log10(df3["russian_r_cfd"])
df3.loc[df3.index[3], "austin_c"] = 0
df3.head()

[48]:

site_no	russian_r	austin_c	year	russian_r_cfd	russian_r_af	austin_c_cfd	austin_c_af	day_of_year	russian_bf_af	baseflow_trend
datetime
1939-10-01 00:00:00+00:00	226.717173	999.0	1939	7.203685	366.942991	NaN	NaN	274	366.942991	NaN
1939-10-02 00:00:00+00:00	2.267172	NaN	1939	7.203685	366.942991	NaN	NaN	275	366.942991	NaN
1939-10-03 00:00:00+00:00	2.267172	NaN	1939	7.203685	366.942991	NaN	NaN	276	366.942991	NaN
1939-10-04 00:00:00+00:00	2.267172	0.0	1939	7.203685	366.942991	NaN	NaN	277	366.942991	NaN
1939-10-05 00:00:00+00:00	2.267172	NaN	1939	7.203685	366.942991	NaN	NaN	278	366.942991	NaN

Now for some powerful analysis using fourier analysis to extract the data’s signal.

Some background for your evening viewing: https://youtu.be/spUNpyF58BY

We have to detrend the data for fast fourier transforms to work properly. Here’s a discussion on why:

https://groups.google.com/forum/#!topic/comp.dsp/kYDZqetr_TU

Fortunately we can easily do this in python using scipy!

https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.detrend.html

Let’s create a new dataframe with only the data we’re interested in analysing.

[49]:

df_data = df2[["russian_r_af", "year"]]
df_data = df_data.rename(columns={"russian_r_af": "Q"})
df_data.describe()

[49]:

site_no	Q	year
count	30773.000000	30773.000000
mean	4254.981092	1980.626036
std	11328.372092	24.322069
min	1.487607	1939.000000
25%	345.124759	1960.000000
50%	672.398238	1981.000000
75%	2657.857341	2002.000000
max	193785.568837	2023.000000

But first let’s also set the water year by date on this dataframe and drop the single nan value from the dataframe

[50]:

df_data['water_year'] = df_data.index.shift(30+31+31,freq='d').year
df_data.dropna(inplace=True)
df_data["detrended"] = detrend(df_data.Q.values)

/tmp/ipykernel_10068/608845639.py:1: Pandas4Warning: 'd' is deprecated and will be removed in a future version, please use 'D' instead.
  df_data['water_year'] = df_data.index.shift(30+31+31,freq='d').year

[51]:

fig = plt.figure(figsize=(12,6))
ax = plt.subplot(3,1,1)
plt.plot(df_data.detrended)
plt.title('detrended signal')

plt.subplot(3,1,2)
plt.plot(df_data.index, df_data.Q)
plt.title('Raw Signal')

plt.subplot(3,1,3)
plt.plot(df_data.index, df_data.Q - df_data.detrended)
plt.title('Difference')

plt.tight_layout()

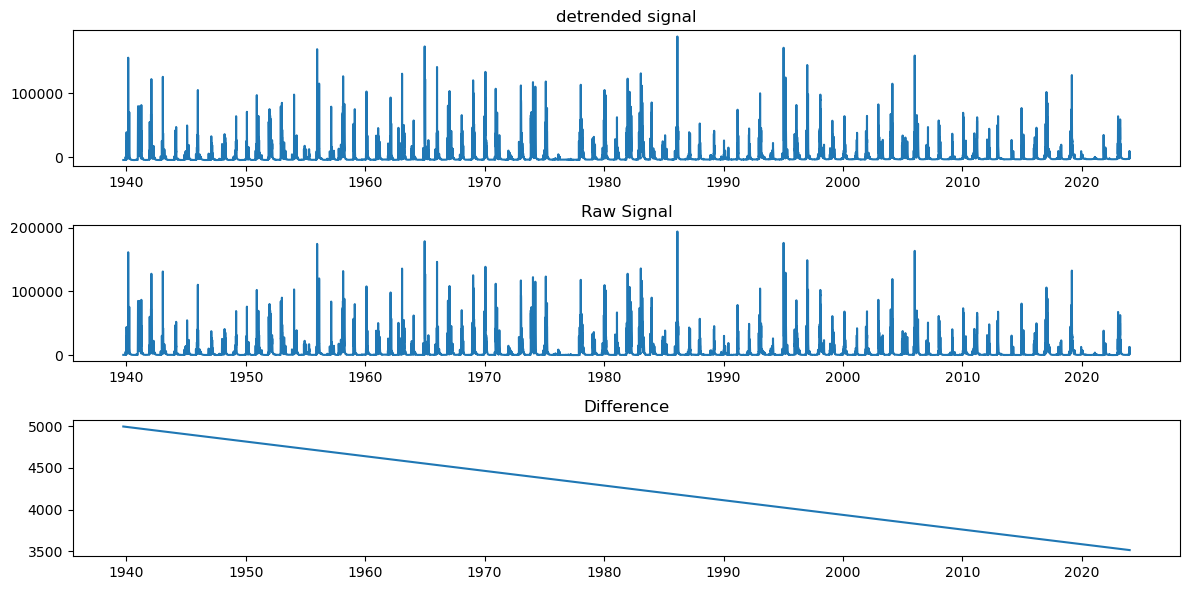
../../../_images/notebooks_part0_python_intro_solutions_08_pandas_104_0.png

Evaluate and plot the Period Spectrum to see timing of recurrence

Here we’ve created a function that performs fast fourier transforms and then plot’s the spectrum for signals of various lengths.

[52]:

def fft_and_plot(df, plot_dominant_periods=4):
    N = len(df)
    yf = np.fft.fft(df.detrended)
    yf = np.abs(yf[:int(N / 2)])

    # get the right frequency
    # https://docs.scipy.org/doc/numpy/reference/generated/numpy.fft.fftfreq.html#numpy.fft.fftfreq
    d = 1. # day
    f = np.fft.fftfreq(N, d)[:int(N/2)]
    f[0] = .00001
    per = 1./f # days

    fig = plt.figure(figsize=(12,6))
    ax = plt.subplot(2,1,1)
    plt.plot(per, yf)
    plt.xscale('log')

    top=np.argsort(yf)[-plot_dominant_periods:]
    j=(10-plot_dominant_periods)/10
    for i in top:
        plt.plot([per[i], per[i]], [0,np.max(yf)], 'r:')
        plt.text(per[i], j*np.max(yf), f"{per[i] :.2f}")
        j+=0.1

    plt.title('Period Spectrum')
    plt.grid()
    ax.set_xlabel('Period (days)')
    plt.xlim([1, 1e4])

    plt.subplot(2,1,2)
    plt.plot(df.index,df.Q)
    plt.title('Raw Signal')
    plt.tight_layout()

Now let’s look at the whole signal

[53]:

fft_and_plot(df_data)

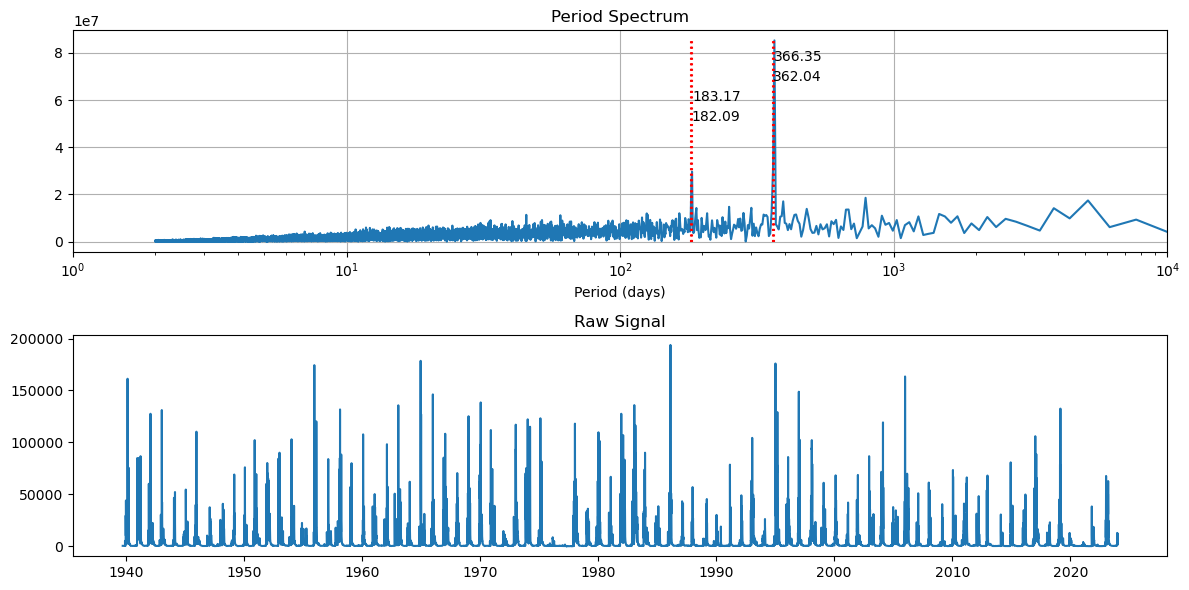
../../../_images/notebooks_part0_python_intro_solutions_08_pandas_108_0.png

We see a strong annual frequency that corresponds to spring snowmelt from the surrounding mountain ranges. The second strongest frequency is biannually, and is likely due to the onset of fall in winter rains

Okay, what about years before dams were installed on the Russian River.

Let’s get in the wayback machine and look at only the years prior to 1954!

[54]:

fft_and_plot(df_data[df_data.index.year < 1954])

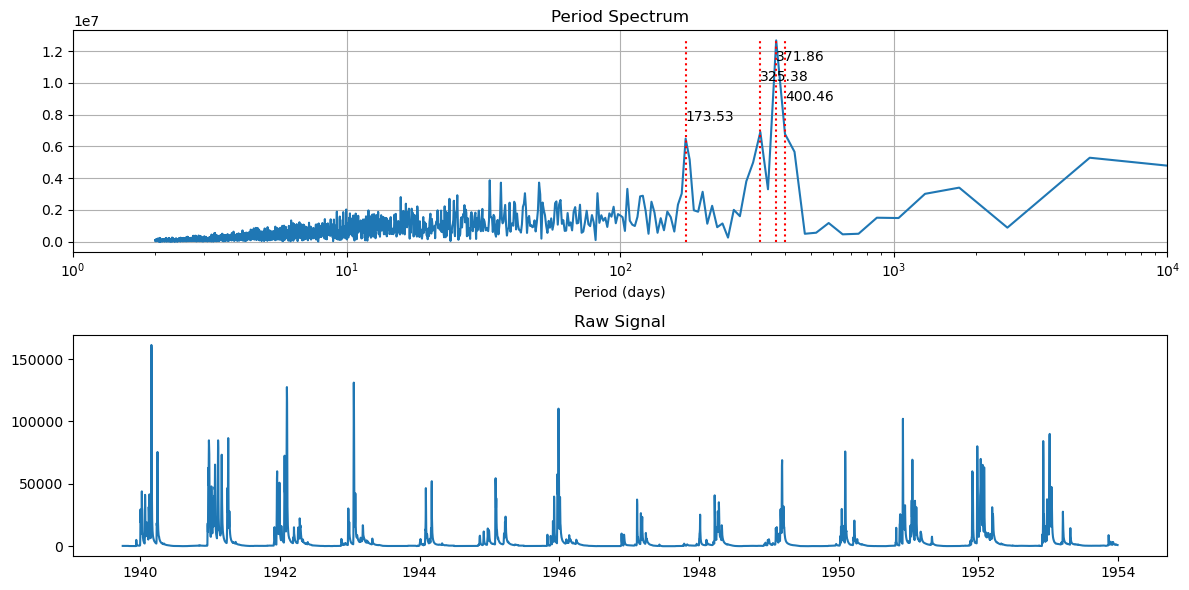
../../../_images/notebooks_part0_python_intro_solutions_08_pandas_111_0.png

The binanual and annual signals have a much wider spread, which suggests that peak runoff was a little more variable in it’s timing compared to the entire data record.

What if we focus in on after 1954?

[55]:

fft_and_plot(df_data[(df_data.index.year > 1954)])

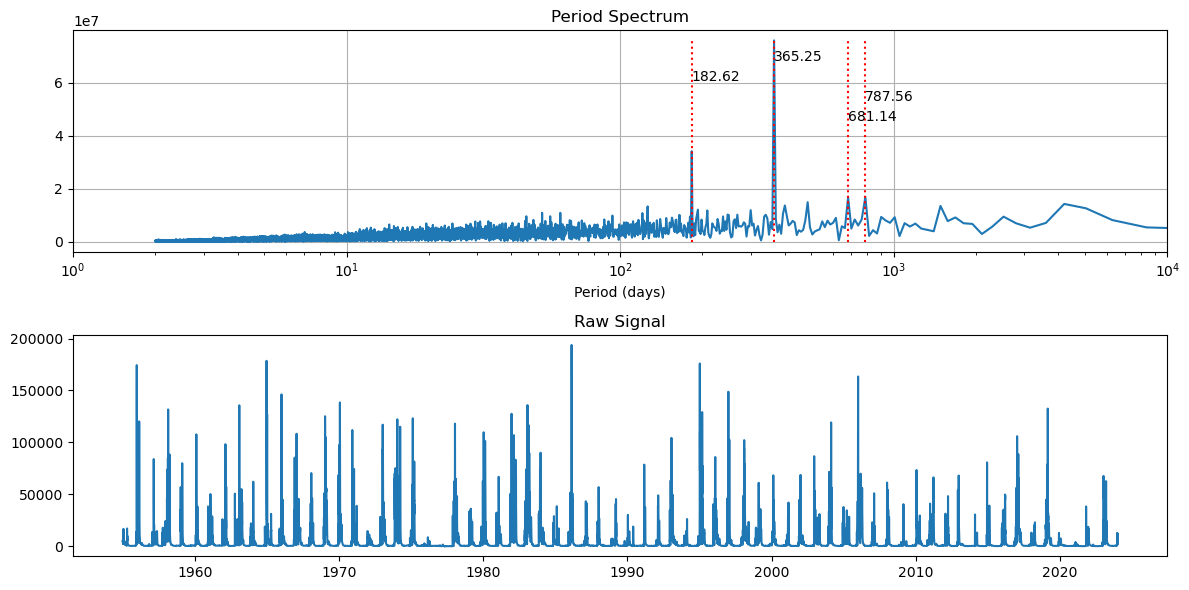
../../../_images/notebooks_part0_python_intro_solutions_08_pandas_114_0.png

It looks like flows are more controlled with a tighter periods.

So post dam construction, flows are much more controlled with regular release schedules.

08: Working with tabular data in Pandas

Not that type of Panda – Python’s Pandas package

Get site information data for part of the Russian River near Guerneville, CA from NWIS

Viewing data in pandas

Getting data from a pandas dataframe

Selection by position

Selection by label

Boolean indexing

Reading and writing data to .csv files

Class exercise 1

Get timeseries data from NWIS for surface water sites

Inspect the data using .plot()

Updating column names

Adding a new column of data to the dataframe

Manipulating data

$ \frac{1 ft^3}{s} \times `:nbsphinx-math:frac{60s}{min}` \times `:nbsphinx-math:frac{60min}{hour}` \times `:nbsphinx-math:frac{24hours}{day}` \rightarrow `:nbsphinx-math:frac{ft^3}{day}` $

Class exercise 2:

groupby: grouping data and performing mathematical operations on it

Joining two DataFrames with an inner join

Stepping back for a minute: exploring Merge and Concat

The merge method

The concat method

Back to working with our climate and stream data

.aggregate()

Class exercise 3: groupy, aggregate, and merge

Baseflow separation

Class exercise 4: baseflow separation

Looking at trends and seasonal cycles in the data with statsmodels

Writing yearly plots of data to a PDF document

Back to the basics:

Adjusting a whole column of data values

updating values by position

updating values based on location

Class exercise 5: setting data

Now for some powerful analysis using fourier analysis to extract the data’s signal.

Evaluate and plot the Period Spectrum to see timing of recurrence

Now let’s look at the whole signal

Okay, what about years before dams were installed on the Russian River.

What if we focus in on after 1954?

Reading and writing data to `.csv` files

Inspect the data using `.plot()`

Joining two `DataFrames` with an inner join

The `merge` method

The `concat` method

`.aggregate()`

Looking at trends and seasonal cycles in the data with `statsmodels`