09: Demonstration of MODFLOW 6 Groundwater Transport with a Voronoi Grid¶
MODFLOW 6 includes a Groundwater Transport (GWT) Model for simulation of solute transport through the subsurface. The GWT Model can be used with structured or unstructured model grids. The purpose of this example is to demonstrate the construction, running, and post-processing of a simple solute transport model.
The solute transport model is based on an existing flow model of the Freyberg example. The flow model usesd a voronoi model grid to simulate steady-state conditions. In this notebook, we create a transient solute transport model using the same voronoi grid that was used for flow.
The following steps are used in this notebook. * Load the existing flow model into FloPy * Plot the model grid * Create the solute transport model * Run the solute transport model with MODFLOW 6 * Create animations of the model results
Imports¶
[1]:
import warnings
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import flopy
from flopy.utils.triangle import Triangle as Triangle
Load and Plot the Existing Flow Model¶
[2]:
model_ws_load = "./data/voronoi/"
model_ws = "./temp/voronoi-gwt/"
name = "voronoi"
name_load = "project"
Load a few shapefiles with geopandas
[3]:
river_shp = "data_project/Flowline_river.shp"
wells_shp = "data_project/pumping_well_locations.shp"
Load the existing voronoi groundwater flow model
[4]:
%%capture
sim = flopy.mf6.MFSimulation.load(sim_ws=model_ws_load, sim_name=name)
Get the gwf model
[5]:
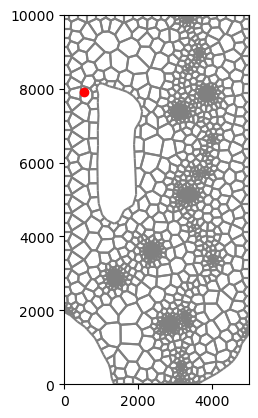
gwf = sim.get_model()
Assign a constant concentration condition to the x, y location of 550, 7900. Use the modelgrid.intersect method to determine the cell number for the constant concentration condition.
[6]:
gwf.modelgrid.intersect(550, 7900)
[6]:
2027
Plot the grid
[7]:
gwf.modelgrid.plot()
ax = plt.gca()
ax.plot(550, 7900, marker="o", lw=0, color="red", )
[7]:
[<matplotlib.lines.Line2D at 0x7f5e5a4e8450>]
Create the Groundwater Transport Model¶
Get data from the GWF DISV package
[8]:
nlay, ncpl = gwf.disv.nlay.array, gwf.disv.ncpl.array
nlay, ncpl
[8]:
(3, 2240)
[9]:
top, botm = gwf.disv.top.array, gwf.disv.botm.array
top.shape, botm.shape
[9]:
((2240,), (3, 2240))
[10]:
nverts = gwf.disv.nvert.array
nverts
[10]:
4908
[11]:
vertices, cell2d = gwf.disv.vertices.array, gwf.disv.cell2d.array
Create the GWT model
[12]:
sim_gwt = flopy.mf6.MFSimulation(sim_name=name, sim_ws=model_ws)
tdis = flopy.mf6.ModflowTdis(sim_gwt,
time_units="days",
perioddata=((10000.0, 100, 1.0),),
)
ims = flopy.mf6.ModflowIms(
sim_gwt,
linear_acceleration="bicgstab",
outer_maximum=200,
inner_maximum=100,
print_option="all",
)
[13]:
gwt = flopy.mf6.ModflowGwt(sim_gwt, modelname=name)
Create the GWT packages
[14]:
dis = flopy.mf6.ModflowGwtdisv(
gwt,
length_units="feet",
nlay=nlay,
ncpl=ncpl,
nvert=nverts,
top=top,
botm=botm,
vertices=vertices,
cell2d=cell2d,
)
ic = flopy.mf6.ModflowGwtic(gwt, strt=0.0)
adv = flopy.mf6.ModflowGwtadv(
gwt,
scheme="tvd",
)
dsp = flopy.mf6.ModflowGwtdsp(gwt, alh=50.0, ath1=5)
mst = flopy.mf6.ModflowGwtmst(gwt, porosity=0.2)
pd = [
("GWFHEAD", f"../../{model_ws_load}{name_load}.hds", None),
("GWFBUDGET", f"../../{model_ws_load}{name_load}.cbc", None),
]
fmi = flopy.mf6.ModflowGwtfmi(gwt, packagedata=pd)
ssm = flopy.mf6.ModflowGwtssm(gwt)
cnc = flopy.mf6.ModflowGwtcnc(gwt, stress_period_data=[(0, 2027, 100.)])
oc = flopy.mf6.ModflowGwtoc(
gwt,
concentration_filerecord=f"{name}.ucn",
saverecord=[("CONCENTRATION", "ALL"),],
printrecord=[("BUDGET", "ALL")],
)
# write the model datasets
sim_gwt.write_simulation()
writing simulation...
writing simulation name file...
writing simulation tdis package...
writing solution package ims_-1...
writing model voronoi...
writing model name file...
writing package disv...
writing package ic...
writing package adv...
writing package dsp...
writing package mst...
writing package fmi...
writing package ssm...
writing package cnc_0...
INFORMATION: maxbound in ('gwt6', 'cnc', 'dimensions') changed to 1 based on size of stress_period_data
writing package oc...
Run the Solute Transport Model¶
[15]:
sim_gwt.run_simulation()
FloPy is using the following executable to run the model: ../../../../../../../../../.local/bin/mf6
MODFLOW 6
U.S. GEOLOGICAL SURVEY MODULAR HYDROLOGIC MODEL
VERSION 6.5.0 05/23/2024
MODFLOW 6 compiled Jun 21 2024 02:57:38 with Intel(R) Fortran Intel(R) 64
Compiler Classic for applications running on Intel(R) 64, Version 2021.7.0
Build 20220726_000000
This software has been approved for release by the U.S. Geological
Survey (USGS). Although the software has been subjected to rigorous
review, the USGS reserves the right to update the software as needed
pursuant to further analysis and review. No warranty, expressed or
implied, is made by the USGS or the U.S. Government as to the
functionality of the software and related material nor shall the
fact of release constitute any such warranty. Furthermore, the
software is released on condition that neither the USGS nor the U.S.
Government shall be held liable for any damages resulting from its
authorized or unauthorized use. Also refer to the USGS Water
Resources Software User Rights Notice for complete use, copyright,
and distribution information.
MODFLOW runs in SEQUENTIAL mode
Run start date and time (yyyy/mm/dd hh:mm:ss): 2024/08/07 19:52:04
Writing simulation list file: mfsim.lst
Using Simulation name file: mfsim.nam
Solving: Stress period: 1 Time step: 1
Solving: Stress period: 1 Time step: 2
Solving: Stress period: 1 Time step: 3
Solving: Stress period: 1 Time step: 4
Solving: Stress period: 1 Time step: 5
Solving: Stress period: 1 Time step: 6
Solving: Stress period: 1 Time step: 7
Solving: Stress period: 1 Time step: 8
Solving: Stress period: 1 Time step: 9
Solving: Stress period: 1 Time step: 10
Solving: Stress period: 1 Time step: 11
Solving: Stress period: 1 Time step: 12
Solving: Stress period: 1 Time step: 13
Solving: Stress period: 1 Time step: 14
Solving: Stress period: 1 Time step: 15
Solving: Stress period: 1 Time step: 16
Solving: Stress period: 1 Time step: 17
Solving: Stress period: 1 Time step: 18
Solving: Stress period: 1 Time step: 19
Solving: Stress period: 1 Time step: 20
Solving: Stress period: 1 Time step: 21
Solving: Stress period: 1 Time step: 22
Solving: Stress period: 1 Time step: 23
Solving: Stress period: 1 Time step: 24
Solving: Stress period: 1 Time step: 25
Solving: Stress period: 1 Time step: 26
Solving: Stress period: 1 Time step: 27
Solving: Stress period: 1 Time step: 28
Solving: Stress period: 1 Time step: 29
Solving: Stress period: 1 Time step: 30
Solving: Stress period: 1 Time step: 31
Solving: Stress period: 1 Time step: 32
Solving: Stress period: 1 Time step: 33
Solving: Stress period: 1 Time step: 34
Solving: Stress period: 1 Time step: 35
Solving: Stress period: 1 Time step: 36
Solving: Stress period: 1 Time step: 37
Solving: Stress period: 1 Time step: 38
Solving: Stress period: 1 Time step: 39
Solving: Stress period: 1 Time step: 40
Solving: Stress period: 1 Time step: 41
Solving: Stress period: 1 Time step: 42
Solving: Stress period: 1 Time step: 43
Solving: Stress period: 1 Time step: 44
Solving: Stress period: 1 Time step: 45
Solving: Stress period: 1 Time step: 46
Solving: Stress period: 1 Time step: 47
Solving: Stress period: 1 Time step: 48
Solving: Stress period: 1 Time step: 49
Solving: Stress period: 1 Time step: 50
Solving: Stress period: 1 Time step: 51
Solving: Stress period: 1 Time step: 52
Solving: Stress period: 1 Time step: 53
Solving: Stress period: 1 Time step: 54
Solving: Stress period: 1 Time step: 55
Solving: Stress period: 1 Time step: 56
Solving: Stress period: 1 Time step: 57
Solving: Stress period: 1 Time step: 58
Solving: Stress period: 1 Time step: 59
Solving: Stress period: 1 Time step: 60
Solving: Stress period: 1 Time step: 61
Solving: Stress period: 1 Time step: 62
Solving: Stress period: 1 Time step: 63
Solving: Stress period: 1 Time step: 64
Solving: Stress period: 1 Time step: 65
Solving: Stress period: 1 Time step: 66
Solving: Stress period: 1 Time step: 67
Solving: Stress period: 1 Time step: 68
Solving: Stress period: 1 Time step: 69
Solving: Stress period: 1 Time step: 70
Solving: Stress period: 1 Time step: 71
Solving: Stress period: 1 Time step: 72
Solving: Stress period: 1 Time step: 73
Solving: Stress period: 1 Time step: 74
Solving: Stress period: 1 Time step: 75
Solving: Stress period: 1 Time step: 76
Solving: Stress period: 1 Time step: 77
Solving: Stress period: 1 Time step: 78
Solving: Stress period: 1 Time step: 79
Solving: Stress period: 1 Time step: 80
Solving: Stress period: 1 Time step: 81
Solving: Stress period: 1 Time step: 82
Solving: Stress period: 1 Time step: 83
Solving: Stress period: 1 Time step: 84
Solving: Stress period: 1 Time step: 85
Solving: Stress period: 1 Time step: 86
Solving: Stress period: 1 Time step: 87
Solving: Stress period: 1 Time step: 88
Solving: Stress period: 1 Time step: 89
Solving: Stress period: 1 Time step: 90
Solving: Stress period: 1 Time step: 91
Solving: Stress period: 1 Time step: 92
Solving: Stress period: 1 Time step: 93
Solving: Stress period: 1 Time step: 94
Solving: Stress period: 1 Time step: 95
Solving: Stress period: 1 Time step: 96
Solving: Stress period: 1 Time step: 97
Solving: Stress period: 1 Time step: 98
Solving: Stress period: 1 Time step: 99
Solving: Stress period: 1 Time step: 100
Run end date and time (yyyy/mm/dd hh:mm:ss): 2024/08/07 19:52:13
Elapsed run time: 9.034 Seconds
Normal termination of simulation.
[15]:
(True, [])
Post-process the results¶
Use gwt.output. method to get the concentrations. Make an animation the concentrations using flopy.plot methods.
[16]:
head = gwf.output.head().get_data()
spdis = gwf.output.budget().get_data(text="DATA-SPDIS")[0]
qx, qy, qz = flopy.utils.postprocessing.get_specific_discharge(
spdis, gwf, head=gwf.output.head().get_data(),
)
[17]:
times = gwt.output.concentration().get_times()
[18]:
warnings.filterwarnings("ignore")
fig, ax = plt.subplots(figsize=(4, 6), constrained_layout=True)
ax.set_aspect(1)
ax.set_xlabel(r'x')
ax.set_ylabel(r'y')
title = ax.set_title(f"Time = {times[0]} days")
# plot persistent items
vmin, vmax = 1e-3, 100.
norm = colors.LogNorm(vmin=vmin, vmax=vmax)
pmv = flopy.plot.PlotMapView(gwt, ax=ax)
pmv.plot_grid(lw=0.5, color="0.5")
pmv.contour_array(
head,
levels=np.linspace(0, 30, 30),
tri_mask=True,
linestyles="-",
colors="blue",
linewidths=0.5,
)
ca_dict = {
"vmin": vmin,
"vmax": vmax,
"norm": norm,
"masked_values": [0],
}
conc_alldata = gwt.output.concentration().get_alldata()
c = conc_alldata[0]
c[c < vmin] = 0.
cont = pmv.plot_array(c, **ca_dict)
clb = fig.colorbar(
cont,
shrink=0.5,
)
def animate(i):
c = conc_alldata[i].flatten()
c[c < vmin] = 0.
cont.set_array(c)
title = ax.set_title(f"Time = {times[i]} days")
return cont
import matplotlib.animation
ani = matplotlib.animation.FuncAnimation(fig, animate, frames=conc_alldata.shape[0])
plt.close()
from IPython.display import HTML
HTML(ani.to_jshtml())
# can use this command to write animation to file
#ani.save("voronoi-conc-animation.avi")
Animation size has reached 21187051 bytes, exceeding the limit of 20971520.0. If you're sure you want a larger animation embedded, set the animation.embed_limit rc parameter to a larger value (in MB). This and further frames will be dropped.
[18]: