03: Loading and visualizing groundwater models

This exercise, we will load an existing model using Flopy, look at some of the inputs, run the model, and load and plot some of the results.

The Pleasant Lake example

The example model is a simplified version of the MODFLOW-6 model published by Fienen and others (2022, 2021), of the area around Pleasant Lake in central Wisconsin, USA. The original report and model files are available at the links below.

Example model details:

  • Transient MODFLOW-6 simulation with monthly stress periods for calendar year 2012

  • units of meters and days

  • 4 layers; 100 meter uniform grid spacing

    • layers 1-3 represent surficial deposits

    • layer 4 represents Paleozoic bedrock (sandstone)

  • Transient specified head perimeter boundary (CHD package) from a regional model solution

  • Transient recharge from a soil water balance model, specified with RCHA

  • Streams specified with SFR

  • Pleasant Lake simulated with the Lake Package

  • Head observations specified with the OBS utility

[1]:

from pathlib import Path
import flopy
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

[2]:

# make an output folder
output_folder = Path('03-output')
output_folder.mkdir(exist_ok=True)

load a preexisting MODFLOW 6 model

Because this is MODFLOW 6, we need to load the simulation first, and then get the model.

Note: To avoid loading certain packages (that may be slow) use the load_only argument to specify the packages that should be loaded.
e.g. load_only=['dis']
[3]:

%%capture
sim_ws = Path('../data/pleasant-lake/')
sim = flopy.mf6.MFSimulation.load('pleasant', sim_ws=str(sim_ws), exe_name='mf6',
                                  #load_only=['dis']
                         )
sim.model_names

[4]:

model = sim.get_model('pleasant')
Visualizing the model

First let’s check that the model grid is correctly located. It is, in this case, because the model has the origin and rotation specified in the DIS package.

[5]:

model.modelgrid

[5]:

xll:552400.0; yll:387200.0; rotation:0.0; units:meters; lenuni:2

[6]:

model.get_package_list()

[6]:

['DIS',
 'IC',
 'NPF',
 'STO',
 'RCHA_0',
 'OC',
 'CHD_OBS',
 'CHD_0',
 'SFR_OBS',
 'SFR_0',
 'LAK_OBS',
 'LAK_LAKTAB',
 'LAK_0',
 'WEL_0',
 'OBS_3']

However, in order to write shapefiles with a .prj file that specifies the coordinate references system (CRS), we need to assign one to the grid (there currently is no CRS input for MODFLOW 6). We can do this by simply specifying an EPSG code to the crs attribute (in this case 3070 for Wisconsin Transverse Mercator).

[7]:

model.modelgrid.crs = 3070
model.modelgrid.units

[7]:

'meters'

Let’s also assign the modelgrid to a variable so we don’t have to type model.modelgrid every time

[8]:

modelgrid = model.modelgrid

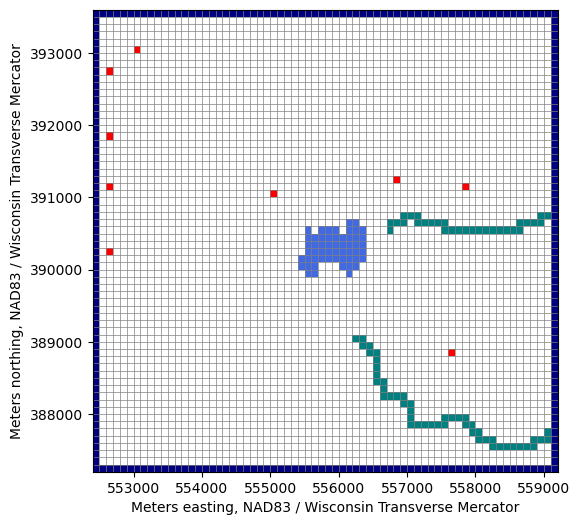
On a map

We can plot the model in the CRS using the PlotMapView object. More examples in the Flopy demo here (for unstructured grids too!): https://github.com/modflowpy/flopy/blob/develop/examples/Notebooks/flopy3.3_PlotMapView.ipynb

[9]:

fig, ax = plt.subplots(figsize=(6, 6))
pmv = flopy.plot.PlotMapView(model, ax=ax)
lc = pmv.plot_grid(lw=0.5)
pmv.plot_bc("WEL", plotAll=True)
pmv.plot_bc("LAK", plotAll=True)
pmv.plot_bc("SFR", plotAll=True)
pmv.plot_bc("CHD", plotAll=True)
ax.set_xlabel(f'{modelgrid.units.capitalize()} easting, {modelgrid.crs.name}')
ax.set_ylabel(f'{modelgrid.units.capitalize()} northing, {modelgrid.crs.name}')

[9]:

Text(0, 0.5, 'Meters northing, NAD83 / Wisconsin Transverse Mercator')
../../../_images/notebooks_part1_flopy_solutions_03_Loading_and_visualizing_models-solutions_14_1.png 
[10]:

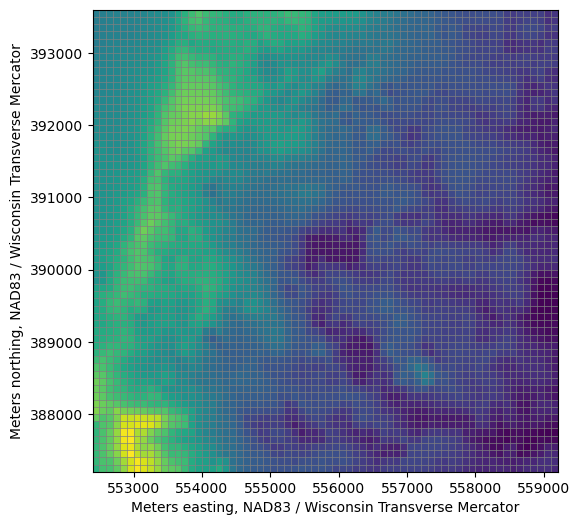
fig, ax = plt.subplots(figsize=(6, 6))
pmv = flopy.plot.PlotMapView(model, ax=ax)
lc = pmv.plot_grid(lw=0.5)
top = pmv.plot_array(model.dis.top.array)
ax.set_xlabel(f'{modelgrid.units.capitalize()} easting, {modelgrid.crs.name}')
ax.set_ylabel(f'{modelgrid.units.capitalize()} northing, {modelgrid.crs.name}')

[10]:

Text(0, 0.5, 'Meters northing, NAD83 / Wisconsin Transverse Mercator')
../../../_images/notebooks_part1_flopy_solutions_03_Loading_and_visualizing_models-solutions_15_1.png

Exporting the model grid to a shapefile

[11]:

modelgrid.write_shapefile(str(output_folder / 'pleasant_grid.shp'))

Get the model grid as a GeoPandas GeoDataFrame

[12]:

modelgrid_gdf = modelgrid.geo_dataframe
modelgrid_gdf

[12]:
geometry
0 POLYGON ((552400 393600, 552400 393500, 552500...
1 POLYGON ((552500 393600, 552500 393500, 552600...
2 POLYGON ((552600 393600, 552600 393500, 552700...
3 POLYGON ((552700 393600, 552700 393500, 552800...
4 POLYGON ((552800 393600, 552800 393500, 552900...
... ...
4347 POLYGON ((558700 387300, 558700 387200, 558800...
4348 POLYGON ((558800 387300, 558800 387200, 558900...
4349 POLYGON ((558900 387300, 558900 387200, 559000...
4350 POLYGON ((559000 387300, 559000 387200, 559100...
4351 POLYGON ((559100 387300, 559100 387200, 559200...

4352 rows × 1 columns

Add row, column information to model grid GeoDataFrame

[13]:

modelgrid.shape

[13]:

(4, 64, 68)

[14]:

modelgrid_gdf['i'] = modelgrid_gdf.index // modelgrid.ncol
modelgrid_gdf['j'] = modelgrid_gdf.index % modelgrid.ncol
modelgrid_gdf

[14]:
geometry i j
0 POLYGON ((552400 393600, 552400 393500, 552500... 0 0
1 POLYGON ((552500 393600, 552500 393500, 552600... 0 1
2 POLYGON ((552600 393600, 552600 393500, 552700... 0 2
3 POLYGON ((552700 393600, 552700 393500, 552800... 0 3
4 POLYGON ((552800 393600, 552800 393500, 552900... 0 4
... ... ... ...
4347 POLYGON ((558700 387300, 558700 387200, 558800... 63 63
4348 POLYGON ((558800 387300, 558800 387200, 558900... 63 64
4349 POLYGON ((558900 387300, 558900 387200, 559000... 63 65
4350 POLYGON ((559000 387300, 559000 387200, 559100... 63 66
4351 POLYGON ((559100 387300, 559100 387200, 559200... 63 67

4352 rows × 3 columns

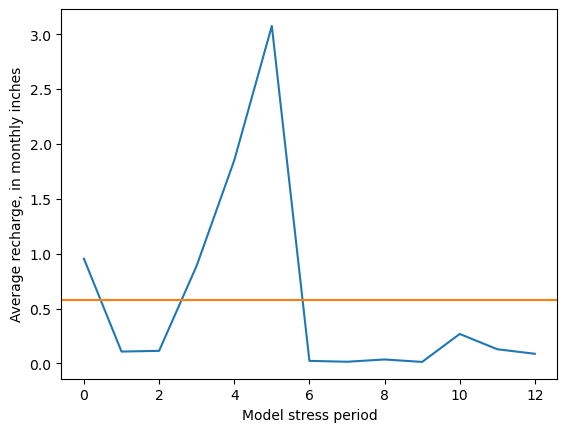
more examples in the Flopy demo here: https://github.com/modflowpy/flopy/blob/develop/examples/Notebooks/flopy3.3_PlotCrossSection.ipynb

By row or column

[15]:

fig, ax = plt.subplots(figsize=(14, 5))
xs = flopy.plot.PlotCrossSection(model=model, line={"row": 30}, ax=ax)
lc = xs.plot_grid()
xs.plot_bc("LAK")
xs.plot_bc("SFR")
ax.set_xlabel(f'Distance, in {modelgrid.units.capitalize()}')
ax.set_ylabel(f'Elevation, in {modelgrid.units.capitalize()}')

[15]:

Text(0, 0.5, 'Elevation, in Meters')
../../../_images/notebooks_part1_flopy_solutions_03_Loading_and_visualizing_models-solutions_25_1.png

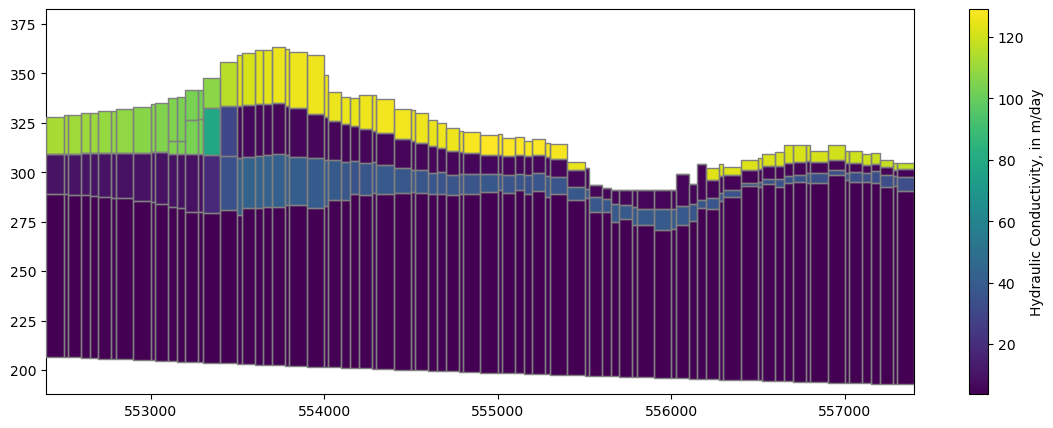
Along an arbitrary line

(and in Geographic Coordinates)

[16]:

fig, ax = plt.subplots(figsize=(14, 5))
xs_line = [(552400, 393000), (552400 + 5000, 393000 - 4000)]
xs = flopy.plot.PlotCrossSection(model=model,
                                 line={"line": xs_line}, ax=ax,
                                 geographic_coords=True)
lc = xs.plot_grid(zorder=4)

pc = xs.plot_array(model.npf.k.array)
fig.colorbar(pc, label='Hydraulic Conductivity, in m/day');
../../../_images/notebooks_part1_flopy_solutions_03_Loading_and_visualizing_models-solutions_27_0.png

What if we want to look at cross sections for each row or column?

This code allows for every row or column to be visualized in cross section within the Jupyter Notebook session.

[17]:

fig, ax = plt.subplots(figsize=(14, 5))
frames = modelgrid.shape[1] # set frames to number of rows

def update(i):
    ax.cla()
    xs = flopy.plot.PlotCrossSection(model=model, line={"row": i}, ax=ax)
    lc = xs.plot_grid()
    xs.plot_bc("LAK")
    xs.plot_bc("SFR")
    ax.set_title(f"row: {i}")
    ax.set_xlabel(f'Distance, in {modelgrid.units.capitalize()}')
    ax.set_ylabel(f'Elevation, in {modelgrid.units.capitalize()}')
    return

import matplotlib.animation as animation
ani = animation.FuncAnimation(fig=fig, func=update, frames=frames)
plt.close()

from IPython.display import HTML
HTML(ani.to_jshtml())

[17]:

Every input to MODFOW is attached to a Flopy object (with the attribute name of the variable) as a numpy ndarray (for ndarray-type data) or a recarray for tabular or list-type data. For example, we can access the recharge array (4D– nper x nlay x nrow x ncol) with:

model.rcha.recharge.array

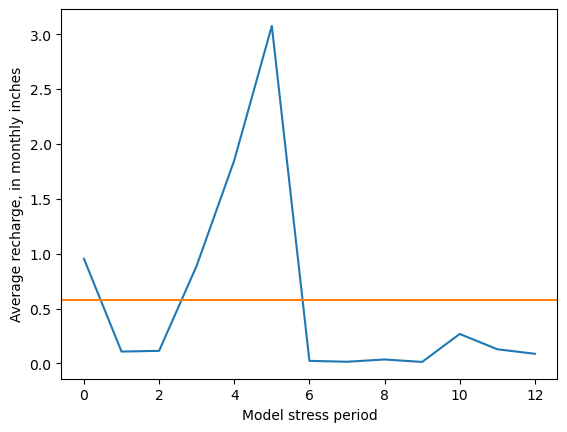
ndarray example: plot spatial average recharge by stress period

To minimize extra typing, it often makes sense to reassign the numpy array to a new variable to work with it further.

[18]:

rch_inches = model.rcha.recharge.array[:, 0, :, :].mean(axis=(1, 2)) * 12 * 30.4 / .3048
fig, ax = plt.subplots()
ax.plot(rch_inches)
ax.axhline(rch_inches.mean(), c='C1')
ax.set_ylabel(f"Average recharge, in monthly inches")
ax.set_xlabel("Model stress period")

[18]:

Text(0.5, 0, 'Model stress period')
../../../_images/notebooks_part1_flopy_solutions_03_Loading_and_visualizing_models-solutions_32_1.png

Tabular data example: plot pumping by stress period

Most tabular input for the ‘basic’ stress packages (Constant Head, Drain, General Head, RIV, WEL, etc) are accessible via a stress_period_data attribute.

  • To access the data, we have to call another .data attribute, which gives us a dictionary of recarrays by stress period.

  • Any one of these can be converted to a pandas.DataFrame individually, or we can make a dataframe of all of them with a simple loop.

[19]:

dfs = []
for kper, df in model.wel.stress_period_data.get_dataframe().items():
    df['per'] = kper
    dfs.append(df)
df = pd.concat(dfs)
df.head()

[19]:
cellid_layer cellid_row cellid_column q boundname per
0 2 24 2 -396.867 pleasant_2-13-2 0
1 2 17 2 -409.900 pleasant_2-9-2 0
2 3 23 44 0.000 pleasant_3-12-23 0
3 3 25 26 0.000 pleasant_3-13-14 0
4 3 24 54 -878.654 pleasant_3-13-28 0

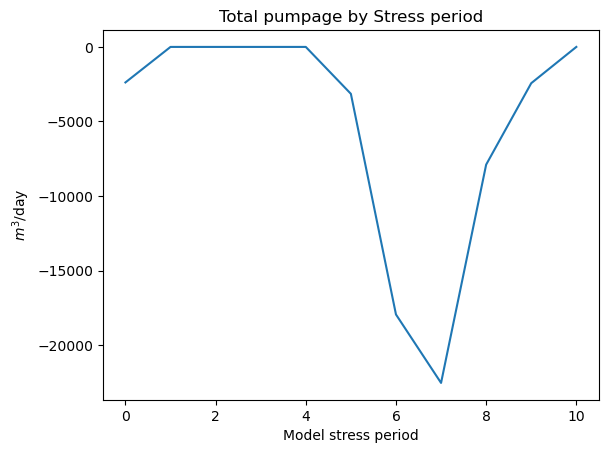
Now we can sum by stress period, or plot individual wells across stress periods

[20]:

df.groupby('per').sum()['q'].plot()
plt.title('Total pumpage by Stress period')
plt.ylabel('$m^3$/day')
plt.xlabel('Model stress period')

[20]:

Text(0.5, 0, 'Model stress period')
../../../_images/notebooks_part1_flopy_solutions_03_Loading_and_visualizing_models-solutions_36_1.png

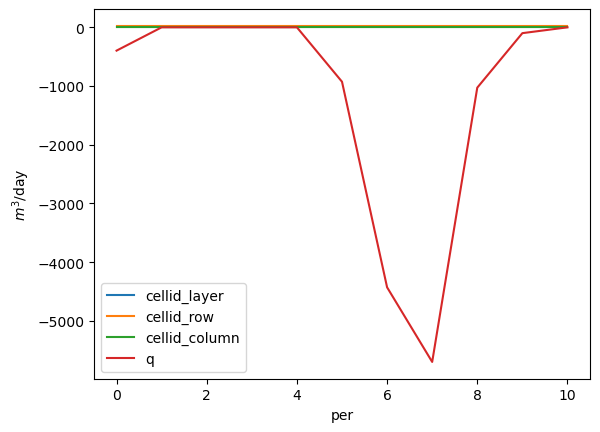
About many gallons did this well pump in stress periods 1 through 12?

[21]:

ax = df.groupby('boundname').get_group('pleasant_2-13-2').plot(x='per')
ax.set_ylabel('$m^3$/day')

[21]:

Text(0, 0.5, '$m^3$/day')
../../../_images/notebooks_part1_flopy_solutions_03_Loading_and_visualizing_models-solutions_38_1.png

Solution:

  1. get the pumping rates by stress period

[22]:

rates = df.groupby('boundname').get_group('pleasant_2-13-2')[1:]
rates

[22]:
cellid_layer cellid_row cellid_column q boundname per
0 2 24 2 0.0000 pleasant_2-13-2 1
0 2 24 2 0.0000 pleasant_2-13-2 4
0 2 24 2 -926.7360 pleasant_2-13-2 5
0 2 24 2 -4428.3600 pleasant_2-13-2 6
0 2 24 2 -5699.1800 pleasant_2-13-2 7
0 2 24 2 -1027.5000 pleasant_2-13-2 8
0 2 24 2 -99.1399 pleasant_2-13-2 9
0 2 24 2 0.0000 pleasant_2-13-2 10

  1. Google “python get days in month” or similar (simply using 30.4 would be fine too for an approximate answer)

[23]:

import calendar
rates['days'] = [calendar.monthrange(2012,m)[1] for m in rates['per']]

  1. multiply the days by the daily pumping rate to get the totals; convert units and sum

[24]:

rates

[24]:
cellid_layer cellid_row cellid_column q boundname per days
0 2 24 2 0.0000 pleasant_2-13-2 1 31
0 2 24 2 0.0000 pleasant_2-13-2 4 30
0 2 24 2 -926.7360 pleasant_2-13-2 5 31
0 2 24 2 -4428.3600 pleasant_2-13-2 6 30
0 2 24 2 -5699.1800 pleasant_2-13-2 7 31
0 2 24 2 -1027.5000 pleasant_2-13-2 8 31
0 2 24 2 -99.1399 pleasant_2-13-2 9 30
0 2 24 2 0.0000 pleasant_2-13-2 10 31 
[25]:

rates['gallons'] = rates['q'] * rates['days'] * 264.172
print(f"{rates['gallons'].sum():,}")

-98,557,525.66559602

[26]:

sim.run_simulation()

FloPy is using the following executable to run the model: ../../../../../../../../../.local/bin/mf6
                                   MODFLOW 6
                U.S. GEOLOGICAL SURVEY MODULAR HYDROLOGIC MODEL
                            VERSION 6.6.2 05/12/2025

   MODFLOW 6 compiled May 24 2025 11:41:46 with Intel(R) Fortran Intel(R) 64
   Compiler Classic for applications running on Intel(R) 64, Version 2021.7.0
                             Build 20220726_000000

This software has been approved for release by the U.S. Geological
Survey (USGS). Although the software has been subjected to rigorous
review, the USGS reserves the right to update the software as needed
pursuant to further analysis and review. No warranty, expressed or
implied, is made by the USGS or the U.S. Government as to the
functionality of the software and related material nor shall the
fact of release constitute any such warranty. Furthermore, the
software is released on condition that neither the USGS nor the U.S.
Government shall be held liable for any damages resulting from its
authorized or unauthorized use. Also refer to the USGS Water
Resources Software User Rights Notice for complete use, copyright,
and distribution information.


 MODFLOW runs in SEQUENTIAL mode

 Run start date and time (yyyy/mm/dd hh:mm:ss): 2025/09/26 14:26:56

 Writing simulation list file: mfsim.lst
 Using Simulation name file: mfsim.nam

    Solving:  Stress period:     1    Time step:     1
    Solving:  Stress period:     2    Time step:     1
    Solving:  Stress period:     3    Time step:     1
    Solving:  Stress period:     4    Time step:     1
    Solving:  Stress period:     5    Time step:     1
    Solving:  Stress period:     6    Time step:     1
    Solving:  Stress period:     7    Time step:     1
    Solving:  Stress period:     8    Time step:     1
    Solving:  Stress period:     9    Time step:     1
    Solving:  Stress period:    10    Time step:     1
    Solving:  Stress period:    11    Time step:     1
    Solving:  Stress period:    12    Time step:     1
    Solving:  Stress period:    13    Time step:     1

 Run end date and time (yyyy/mm/dd hh:mm:ss): 2025/09/26 14:26:58
 Elapsed run time:  2.412 Seconds


WARNING REPORT:

  1. OPTIONS BLOCK VARIABLE 'UNIT_CONVERSION' IN FILE 'pleasant.sfr' WAS
     DEPRECATED IN VERSION 6.4.2. SETTING UNIT_CONVERSION DIRECTLY.
 Normal termination of simulation.

[26]:

(True, [])

Getting MODFLOW output from the model object

With MODFLOW 6 models, we can get the output from the model object, without having to reference the output files.

In Flopy, MODFLOW binary output is read using objects that represent the various file types.

[27]:

headfile_object = model.output.head()
headfile_object

[27]:

<flopy.utils.binaryfile.HeadFile at 0x7f357cbebf10>

The output file objects include various methods and attributes with information about the output. For example, the elapsed simulation times with output recrods.

[28]:

headfile_object.get_times()

[28]:

[np.float64(1.0),
 np.float64(32.0),
 np.float64(61.0),
 np.float64(92.0),
 np.float64(122.0),
 np.float64(153.0),
 np.float64(183.0),
 np.float64(214.0),
 np.float64(245.0),
 np.float64(275.0),
 np.float64(306.0),
 np.float64(336.0),
 np.float64(367.0)]

Including a get_data() method to get the output values:

[29]:

heads = headfile_object.get_data(kstpkper=(0, 0))

[30]:

sfr_output_object = model.sfr.output
sfr_output_object

[30]:

MF6Output Class for sfr_0
Available output methods include:
.zonebudget()
.budget()
.budgetcsv()
.package_convergence()
.obs()
.stage()

[31]:

sfr_stage = sfr_output_object.stage().get_data()[0, 0, :]

Cell Budget output works the same way.

In this case, we specified save_flows as an option in the various packages to save flux output for those packages, include fluxes to and from the Lake and SFR Packages.

[32]:

cbc_file_object = model.output.budget()
cbc_file_object.get_unique_record_names()

[32]:

[np.bytes_(b'          STO-SS'),
 np.bytes_(b'          STO-SY'),
 np.bytes_(b'    FLOW-JA-FACE'),
 np.bytes_(b'             WEL'),
 np.bytes_(b'            RCHA'),
 np.bytes_(b'             CHD'),
 np.bytes_(b'             SFR'),
 np.bytes_(b'             LAK')]

Cell Budget results are returned in a list that allows for auxilliary information besides the output to be included in subsequent items.

The values are the first item.

[33]:

lake_fluxes = cbc_file_object.get_data(text='lak', full3D=True)[0]

Especially for structured (layer, row, column) grids, we usually want to specify full3D=True. This returns the results in a 3D Numpy array.

Otherwise, results are returned in a Numpy recarray, referenced by unique node numbers.

[34]:

cbc_file_object.get_data(text='lak')[0][:5]

[34]:

rec.array([(6560, 1, -163.5854572 ), (6566, 1,   85.47697217),
           (6763, 1, -201.692521  ), (6633, 1,   53.84431952),
           (6563, 1,   -8.88752784)],
          dtype=[('node', '<i4'), ('node2', '<i4'), ('q', '<f8')])

[35]:

cbc_file_object = model.output.budget()
lake_fluxes = cbc_file_object.get_data(text='lak', full3D=True)[0].sum(axis=0)
sfr_fluxes = cbc_file_object.get_data(text='sfr', full3D=True)[0]

Alternatively, read MODFLOW binary output from the files

[36]:

from flopy.utils import binaryfile as bf

headfile_object = bf.HeadFile(sim_ws / f"{model.name}.hds")
heads_from_the_file = headfile_object.get_data(kstpkper=(0, 0))

[37]:

cbc_file_object = bf.CellBudgetFile(sim_ws / f"{model.name}.cbc")
cbc_fluxes_from_the_file = cbc_file_object.get_data(kstpkper=(0, 0), full3D=True)[0]

MODFLOW 6 CSV observation output can also be easily read using pandas

[38]:

lak_output = pd.read_csv(sim_ws / 'lake1.obs.csv')
lak_output.head()

[38]:
time STAGE INFLOW RAINFALL RUNOFF LAK WITHDRAWAL EVAPORATION STORAGE VOLUME SURFACE-AREA WETTED-AREA CONDUCTANCE
0 1.0 302.000818 0.0 2048.465617 0.0 1432.796191 0.0 -480.872306 0.000000 4820408.264 763500.0 540000.0 13694.60149
1 32.0 301.950066 0.0 494.206161 0.0 1499.121637 0.0 -196.705306 1249.989555 4781658.588 763500.0 540000.0 13694.60149
2 61.0 301.903708 0.0 668.720690 0.0 1511.548756 0.0 -311.952356 1220.489893 4746264.381 763500.0 540000.0 13694.60149
3 92.0 301.884950 0.0 1851.709161 0.0 1368.143521 0.0 -873.164663 461.989594 4731942.704 763500.0 540000.0 13694.60149
4 122.0 301.889281 0.0 2333.612300 0.0 1096.265713 0.0 -1055.726856 -110.223034 4735249.395 763500.0 540000.0 13694.60149 
[39]:

head_obs_output = pd.read_csv(sim_ws / f"{model.name}.head.obs")
head_obs_output.head()

[39]:
time 00400037_UWSP 00400037_UWSP.1 00400037_UWSP.2 00400037_UWSP.3 00400041_UWSP 00400041_UWSP.1 00400041_UWSP.2 00400041_UWSP.3 10019264_LK ... YH229.2 YH229.3 YQ987 YQ987.1 YQ987.2 YQ987.3 YS864 YS864.1 YS864.2 YS864.3
0 1.0 310.161509 310.152440 310.146632 309.972583 294.571188 294.533753 294.507520 294.460828 287.057064 ... 301.671867 301.833545 302.314533 302.324774 302.335628 302.712518 312.448733 312.427510 312.400785 312.395162
1 32.0 310.114717 310.114717 310.108406 309.932164 294.496467 294.460880 294.436082 294.403306 287.002266 ... 301.609129 301.772555 302.230838 302.244670 302.258673 302.652591 312.387007 312.383407 312.353905 312.348160
2 61.0 310.078745 310.078745 310.072239 309.894409 294.432037 294.396652 294.372019 294.340104 286.969376 ... 301.559509 301.721138 302.179090 302.193726 302.208416 302.605806 312.345221 312.339465 312.307319 312.299521
3 92.0 310.051664 310.051664 310.048010 309.878756 294.459305 294.424027 294.399453 294.367593 287.008239 ... 301.576502 301.736277 302.211276 302.221966 302.233239 302.614153 312.367330 312.340335 312.309477 312.304597
4 122.0 310.100468 310.085611 310.082751 309.915603 294.568056 294.532587 294.507949 294.476668 287.084117 ... 301.647729 301.809016 302.261779 302.269823 302.278917 302.655915 312.416061 312.379106 312.355470 312.358140

5 rows × 550 columns

The head solution is reported for each layer.

  • We can use the get_water_table utility to get a 2D surface of the water table position in each cell.

  • To accurately portray the water table around the lake, we can read the lake stage from the observation file and assign it to the relevant cells in the water table array.

  • Otherwise, depending on how the lake is constructed, the lake area would be shown as a nodata/no-flow area, or as the heads in the groundwater system below the lakebed.

  • In this case, we are getting the solution from the initial steady-state period

[40]:

from flopy.utils.postprocessing import get_water_table

water_table = get_water_table(heads)

# add the lake stage to the water table
stage = lak_output['STAGE'][0]
cnd = pd.DataFrame(model.lak.connectiondata.array)
k, i, j = zip(*cnd['cellid'])
water_table[i, j] = stage
# add the SFR stage as well
# get the SFR cell i, j locations
# by unpacking the cellid tuples in the packagedata
sfr_k, sfr_i, sfr_j = zip(*model.sfr.packagedata.array['cellid'])
water_table[sfr_i, sfr_j] = sfr_stage

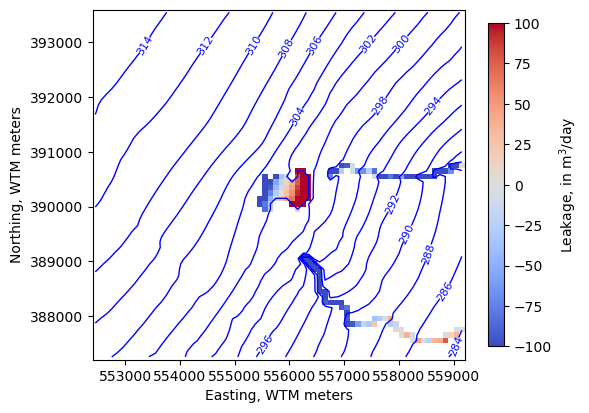
We can add output to a PlotMapView instance as arrays

[41]:

levels=np.arange(280, 315, 2)

fig, ax = plt.subplots(figsize=(6, 6))
pmv = flopy.plot.PlotMapView(model, ax=ax)
ctr = pmv.contour_array(water_table, levels=levels,
                        linewidths=1, colors='b')
labels = pmv.ax.clabel(ctr, inline=True, fontsize=8, inline_spacing=1)
vmin, vmax = -100, 100
im = pmv.plot_array(lake_fluxes, cmap='coolwarm', vmin=vmin, vmax=vmax)
im = pmv.plot_array(sfr_fluxes.sum(axis=0), cmap='coolwarm', vmin=vmin, vmax=vmax)
cb = fig.colorbar(im, shrink=0.7, label='Leakage, in m$^3$/day')
ax.set_ylabel("Northing, WTM meters")
ax.set_xlabel("Easting, WTM meters")
ax.set_aspect(1)
../../../_images/notebooks_part1_flopy_solutions_03_Loading_and_visualizing_models-solutions_72_0.png

Zoom in on the lake

[42]:

levels=np.arange(280, 315, 1)
new_extent = (554500, 557500, 388500, 392000)

fig, ax = plt.subplots(figsize=(6, 6))
pmv = flopy.plot.PlotMapView(model, ax=ax, extent=new_extent)
ctr = pmv.contour_array(water_table, levels=levels,
                        linewidths=1, colors='b')
labels = pmv.ax.clabel(ctr, inline=True, fontsize=8, inline_spacing=1)
vmin, vmax = -100, 100
im = pmv.plot_array(lake_fluxes, cmap='coolwarm', vmin=vmin, vmax=vmax)
im = pmv.plot_array(sfr_fluxes.sum(axis=0), cmap='coolwarm', vmin=vmin, vmax=vmax)
cb = fig.colorbar(im, shrink=0.7, label='Leakage, in m$^3$/day')
ax.set_ylabel("Northing, WTM meters")
ax.set_xlabel("Easting, WTM meters")
ax.set_aspect(1)
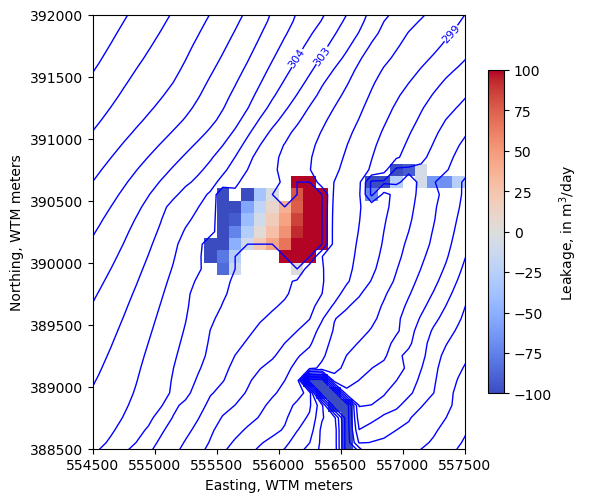
../../../_images/notebooks_part1_flopy_solutions_03_Loading_and_visualizing_models-solutions_74_0.png

We can use the export_array utility to make a GeoTIFF of any 2D array on a structured grid. For example, make a raster of the simulated water table.

[43]:

from flopy.export.utils import export_array

export_array(model.modelgrid, str(output_folder / 'water_table.tif'), water_table)

/home/runner/micromamba/envs/pyclass-docs/lib/python3.11/site-packages/pyproj/crs/crs.py:1295: UserWarning: You will likely lose important projection information when converting to a PROJ string from another format. See: https://proj.org/faq.html#what-is-the-best-format-for-describing-coordinate-reference-systems
  proj = self._crs.to_proj4(version=version)

A common issue with groundwater flow models is overpressurization- where heads above the land surface are simulated. Sometimes, these indicate natural wetlands that aren’t explicitly simulated in the model, but other times they are a sign of unrealistic parameters. Use the information in this lesson to answer the following questions:

  1. Does this model solution have any overpressiuzation? If so, where? Is it appropriate?

  2. What is the maximum value of overpressurization?

  3. What is the maximum depth to water simulated? Where are the greatest depths to water? Do they look appropriate?

Solution

  1. Make a numpy array of overpressurization and get the max and min values

[44]:

op = water_table - model.dis.top.array
op.max(), op.min()

[44]:

(np.float64(11.120818299999996), np.float64(-76.35338698486248))

  1. Plot it

[45]:

plt.imshow(op); plt.colorbar()

[45]:

<matplotlib.colorbar.Colorbar at 0x7f357c5adc10>
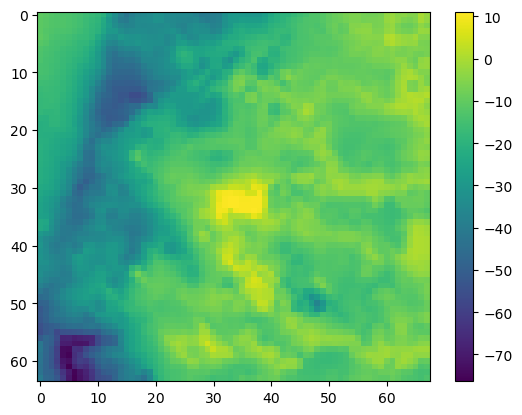
../../../_images/notebooks_part1_flopy_solutions_03_Loading_and_visualizing_models-solutions_81_1.png

  1. Export a raster of overpressurization so we can compare it against air photos (or mapped wetlands if we have them!)

[46]:

export_array(model.modelgrid, str(output_folder / 'op.tif'), op)

The highest levels of overpressurization correspond to Pleasant Lake, where the model top represents the lake bottom. Other areas of OP appear to correspond to lakes or wetlands, especially the spring complex south of Pleasant Lake, where Tagatz Creek originates.

The greatest depths to water correspond to a topographic high in the southwest part of the model domain. A cross section through the area confirms that it is a bedrock high that rises more than 50 meters above the surrounding topography, so a depth to water of 76 meters in this area seems reasonable.

[47]:

fig, ax = plt.subplots(figsize=(10, 3))
xs = flopy.plot.PlotCrossSection(model=model, line={"row": 62}, ax=ax)
lc = xs.plot_grid()
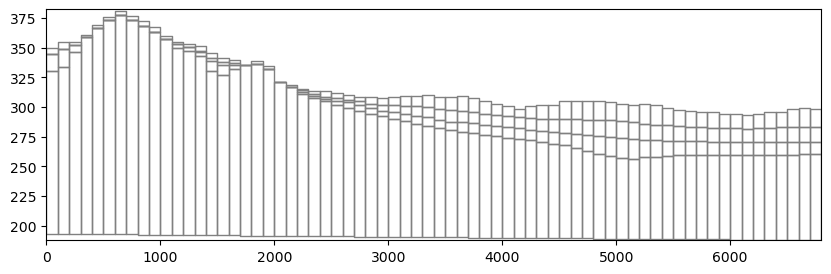
../../../_images/notebooks_part1_flopy_solutions_03_Loading_and_visualizing_models-solutions_85_0.png

We can also view output in cross section. In this case, PlotMatView plots the head solution where the model is saturated. We can add the water table we created above that includes the lake surface.

[48]:

fig, ax = plt.subplots(figsize=(15, 5))
xs_line = [(552400, 393000), (552400 + 5000, 393000 - 4000)]
xs = flopy.plot.PlotCrossSection(model=model,
                                 line={"line": xs_line},
                                 #line={"row": 32},
                                 ax=ax,
                                 geographic_coords=True)
lc = xs.plot_grid()
pc = xs.plot_array(heads, head=heads, alpha=0.5, masked_values=[1e30])
ctr = xs.contour_array(heads, head=heads, levels=levels, colors="b", masked_values=[1e30])
surf = xs.plot_surface(water_table, masked_values=[1e30], color="blue", lw=2)

labels = pmv.ax.clabel(
    ctr, inline=True,
    fontsize=8, inline_spacing=5)

ax.set_xlabel(f'Distance, in {modelgrid.units.capitalize()}')
ax.set_ylabel(f'Elevation, in {modelgrid.units.capitalize()}')

[48]:

Text(0, 0.5, 'Elevation, in Meters')
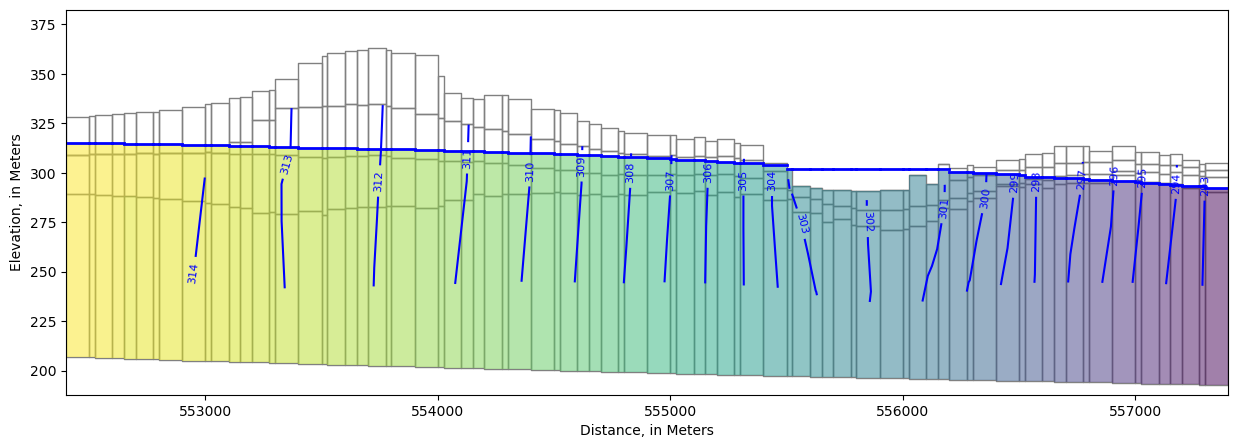
../../../_images/notebooks_part1_flopy_solutions_03_Loading_and_visualizing_models-solutions_87_1.png

In this model, head “observations” were specified at various locations using the MODFLOW 6 Observation Utility. MODFLOW reports simulated values of head at these locations, which can then be compared with equivalent field observations for model parameter estimation.

Earlier we obtained a DataFrame of Lake Package observation output for pleasant lake by reading in ‘lake1.obs.csv’ with pandas. We can read the head observation output with pandas too.

[49]:

headobs = pd.read_csv(sim_ws / 'pleasant.head.obs')
headobs.head()

[49]:
time 00400037_UWSP 00400037_UWSP.1 00400037_UWSP.2 00400037_UWSP.3 00400041_UWSP 00400041_UWSP.1 00400041_UWSP.2 00400041_UWSP.3 10019264_LK ... YH229.2 YH229.3 YQ987 YQ987.1 YQ987.2 YQ987.3 YS864 YS864.1 YS864.2 YS864.3
0 1.0 310.161509 310.152440 310.146632 309.972583 294.571188 294.533753 294.507520 294.460828 287.057064 ... 301.671867 301.833545 302.314533 302.324774 302.335628 302.712518 312.448733 312.427510 312.400785 312.395162
1 32.0 310.114717 310.114717 310.108406 309.932164 294.496467 294.460880 294.436082 294.403306 287.002266 ... 301.609129 301.772555 302.230838 302.244670 302.258673 302.652591 312.387007 312.383407 312.353905 312.348160
2 61.0 310.078745 310.078745 310.072239 309.894409 294.432037 294.396652 294.372019 294.340104 286.969376 ... 301.559509 301.721138 302.179090 302.193726 302.208416 302.605806 312.345221 312.339465 312.307319 312.299521
3 92.0 310.051664 310.051664 310.048010 309.878756 294.459305 294.424027 294.399453 294.367593 287.008239 ... 301.576502 301.736277 302.211276 302.221966 302.233239 302.614153 312.367330 312.340335 312.309477 312.304597
4 122.0 310.100468 310.085611 310.082751 309.915603 294.568056 294.532587 294.507949 294.476668 287.084117 ... 301.647729 301.809016 302.261779 302.269823 302.278917 302.655915 312.416061 312.379106 312.355470 312.358140

5 rows × 550 columns

Head observations can also be accessed via the .output attribute for their respective package. First we have to find the name associated with that package though. We can get this by calling get_package_list(). Looks like "OBS_3" is it (since the only OBS packages in the model is for heads).

[50]:

model.get_package_list()

[50]:

['DIS',
 'IC',
 'NPF',
 'STO',
 'RCHA_0',
 'OC',
 'CHD_OBS',
 'CHD_0',
 'SFR_OBS',
 'SFR_0',
 'LAK_OBS',
 'LAK_LAKTAB',
 'LAK_0',
 'WEL_0',
 'OBS_3']

Next let’s query the available output methods:

[51]:

model.obs_3.output.methods()

[51]:

['obs()']

Now get the output. It comes back as a Numpy recarray be default, but we can easily cast it to a DataFrame.

[52]:

pd.DataFrame(model.obs_3.output.obs().get_data())

[52]:
totim 00400037_UWSP 00400037_UWSP_1 00400037_UWSP_2 00400037_UWSP_3 00400041_UWSP 00400041_UWSP_1 00400041_UWSP_2 00400041_UWSP_3 10019264_LK ... YH229_2 YH229_3 YQ987 YQ987_1 YQ987_2 YQ987_3 YS864 YS864_1 YS864_2 YS864_3
0 1.0 310.161509 310.152440 310.146632 309.972583 294.571188 294.533753 294.507520 294.460828 287.057064 ... 301.671867 301.833545 302.314533 302.324774 302.335628 302.712518 312.448733 312.427510 312.400785 312.395162
1 32.0 310.114717 310.114717 310.108406 309.932164 294.496467 294.460880 294.436082 294.403306 287.002266 ... 301.609129 301.772555 302.230838 302.244670 302.258673 302.652591 312.387007 312.383407 312.353905 312.348160
2 61.0 310.078745 310.078745 310.072239 309.894409 294.432037 294.396652 294.372019 294.340104 286.969376 ... 301.559509 301.721138 302.179090 302.193726 302.208416 302.605806 312.345221 312.339465 312.307319 312.299521
3 92.0 310.051664 310.051664 310.048010 309.878756 294.459305 294.424027 294.399453 294.367593 287.008239 ... 301.576502 301.736277 302.211276 302.221966 302.233239 302.614153 312.367330 312.340335 312.309477 312.304597
4 122.0 310.100468 310.085611 310.082751 309.915603 294.568056 294.532587 294.507949 294.476668 287.084117 ... 301.647729 301.809016 302.261779 302.269823 302.278917 302.655915 312.416061 312.379106 312.355470 312.358140
5 153.0 310.235321 310.199075 310.194833 310.027845 294.796498 294.758553 294.732077 294.686100 287.220264 ... 301.813281 301.975636 302.396360 302.398604 302.402832 302.767035 312.575743 312.507196 312.491556 312.497321
6 183.0 310.163825 310.163825 310.157828 309.981661 294.621679 294.576452 294.544147 294.442276 287.107788 ... 301.718030 301.875807 302.246336 302.255837 302.266475 302.665988 312.425419 312.425419 312.381849 312.318708
7 214.0 310.119995 310.119995 310.112096 309.925188 294.454998 294.409225 294.376607 294.278295 287.028352 ... 301.628453 301.781572 302.117821 302.127804 302.139043 302.556083 312.285063 312.285063 312.219997 312.100432
8 245.0 310.070133 310.070133 310.060672 309.866641 294.339769 294.298032 294.268599 294.199605 286.964157 ... 301.548295 301.700672 302.035369 302.047486 302.060517 302.485163 312.145582 312.145582 312.082348 311.981909
9 275.0 310.017054 310.017054 310.006291 309.806911 294.265782 294.228015 294.201671 294.159662 286.918126 ... 301.480559 301.633655 301.967317 301.980463 301.994352 302.422722 312.023952 312.023952 311.967218 311.886852
10 306.0 309.959204 309.959204 309.947646 309.746573 294.238342 294.205638 294.183002 294.157879 286.889451 ... 301.423747 301.579611 302.097603 302.099598 302.103294 302.453426 311.936403 311.936403 311.895809 311.855302
11 336.0 309.901502 309.901502 309.889458 309.687545 294.192535 294.159201 294.136085 294.109999 286.868051 ... 301.378561 301.534836 301.999046 302.008866 302.019466 302.404509 311.866721 311.866721 311.832468 311.803879
12 367.0 309.841147 309.841147 309.828881 309.627000 294.137787 294.104305 294.081079 294.055085 286.846760 ... 301.335208 301.489307 301.935854 301.949670 301.963715 302.363014 311.801949 311.801949 311.770597 311.747920

13 rows × 550 columns

In MODFLOW 6, we can use boundnames to create observations for groups of cells. For example, in this model, each head value specified in the Constant Head (CHD) Package has a boundname of east, west, north or south, to indicate the side of the model perimeter it’s on.

Example of boundnames specified in an external input file for the CHD Package:

[53]:

pd.read_csv(sim_ws / 'external/chd_001.dat', delim_whitespace=True)

/tmp/ipykernel_13165/614846193.py:1: FutureWarning: The 'delim_whitespace' keyword in pd.read_csv is deprecated and will be removed in a future version. Use ``sep='\s+'`` instead
  pd.read_csv(sim_ws / 'external/chd_001.dat', delim_whitespace=True)

[53]:
#k i j head boundname
0 1 1 68 297.761 east
1 1 2 68 297.475 east
2 1 3 68 297.155 east
3 1 4 68 296.871 east
4 1 5 68 296.628 east
... ... ... ... ... ...
763 4 1 63 299.500 north
764 4 1 64 299.160 north
765 4 1 65 298.815 north
766 4 1 66 298.469 north
767 4 1 67 298.117 north

768 rows × 5 columns

The Constant Head Observation Utility input is then set up like so:

BEGIN options
END options

BEGIN continuous  FILEOUT  pleasant.chd.obs.output.csv
# obsname obstype ID
  east  chd  east
  west  chd  west
  north  chd  north
  south  chd  south
END continuous  FILEOUT  pleasant.chd.obs.output.csv

The resulting observation output (net flow across the boundary faces in model units of cubic meters per day) can be found in pleasant.chd.obs.output.csv:

[54]:

df = pd.read_csv(sim_ws / 'pleasant.chd.obs.output.csv')
df.index = df['time']
df.head()

[54]:
time EAST WEST NORTH SOUTH
time
1.0 1.0 -34777.174522 6212.364587 17421.976405 -9693.413528
32.0 32.0 -34508.241785 6363.316750 17572.839997 -9487.079655
61.0 61.0 -34204.575965 6300.560999 17485.626670 -9557.938536
92.0 92.0 -34234.776102 5908.645868 17351.380660 -9853.130777
122.0 122.0 -34721.889343 5359.082084 17203.878073 -10100.990774

The Mf6ListBudget and MfListBudget (for earlier MODFLOW versions) utilities can assemble the global mass balance output (printed in the Listing file) into a DataFrame. A start_datetime can be added to convert the MODFLOW time to actual dates.

Note: The start_datetime functionality is unaware of steady-state periods, so if we put in the actual model start date of 2012-01-01, the 1-day initial steady-state will be included, resulting in the stress periods being offset by one day. Also note that the dates here represent the end of each stress period.

[55]:

from flopy.utils import Mf6ListBudget

[56]:

mfl = Mf6ListBudget(sim_ws / 'pleasant.list')
flux, vol = mfl.get_dataframes(start_datetime='2011-12-30')
flux.head()

[56]:
STO-SS_IN STO-SY_IN WEL_IN RCHA_IN CHD_IN SFR_IN LAK_IN TOTAL_IN STO-SS_OUT STO-SY_OUT WEL_OUT RCHA_OUT CHD_OUT SFR_OUT LAK_OUT TOTAL_OUT IN-OUT PERCENT_DISCREPANCY
2011-12-31 0.0000 0.000000 0.0 33188.867188 23435.904297 349.638306 3680.284180 60654.695312 0.000000 0.000000 2383.022705 0.0 44272.152344 11781.069336 2217.934814 60654.175781 0.517400 0.0
2012-01-31 6.7081 25877.734375 0.0 3485.810791 23184.136719 518.563782 3719.994385 56792.949219 0.241800 156.215195 0.000000 0.0 43243.300781 11221.008789 2172.376465 56793.144531 -0.195200 -0.0
2012-02-29 6.5506 24792.722656 0.0 3771.585449 23037.080078 680.194580 3735.312012 56023.445312 0.001131 20.584900 0.000000 0.0 43013.406250 10831.583008 2157.964844 56023.539062 -0.094284 -0.0
2012-03-31 0.5149 3190.234619 0.0 30861.951172 23084.673828 687.003601 3648.997559 61473.375000 1.263200 4260.674316 0.000000 0.0 43912.554688 11090.963867 2208.054443 61473.507812 -0.133000 -0.0
2012-04-30 0.0000 0.000000 0.0 64854.593750 22838.197266 377.562012 3493.942871 91564.296875 9.284800 32114.669922 0.000000 0.0 45098.117188 12015.685547 2326.493896 91564.250000 0.044822 0.0 
[57]:

flux.columns

[57]:

Index(['STO-SS_IN', 'STO-SY_IN', 'WEL_IN', 'RCHA_IN', 'CHD_IN', 'SFR_IN',
       'LAK_IN', 'TOTAL_IN', 'STO-SS_OUT', 'STO-SY_OUT', 'WEL_OUT', 'RCHA_OUT',
       'CHD_OUT', 'SFR_OUT', 'LAK_OUT', 'TOTAL_OUT', 'IN-OUT',
       'PERCENT_DISCREPANCY'],
      dtype='object')

[58]:

ax = flux['PERCENT_DISCREPANCY'].plot()
ax.set_ylabel('Percent mass balance error')

[58]:

Text(0, 0.5, 'Percent mass balance error')
../../../_images/notebooks_part1_flopy_solutions_03_Loading_and_visualizing_models-solutions_105_1.png

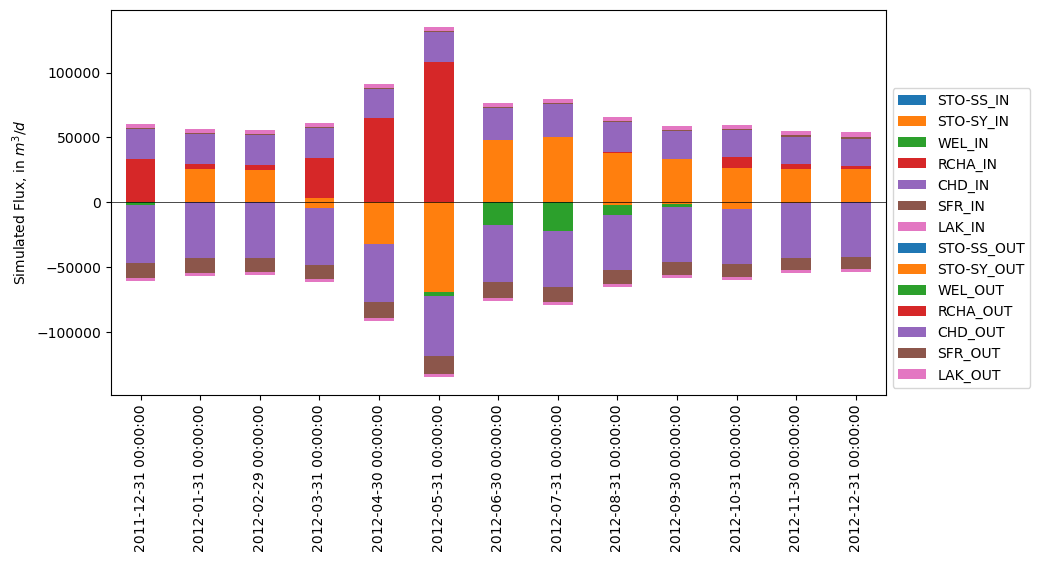
Note: This works best if the in and out columns are aligned, such that STO-SY_IN and STO-SY_OUT are both colored orange, for example.

[59]:

fig, ax = plt.subplots(figsize=(10, 5))
in_cols = ['STO-SS_IN', 'STO-SY_IN', 'WEL_IN', 'RCHA_IN', 'CHD_IN', 'SFR_IN', 'LAK_IN']
out_cols = [c.replace('_IN', '_OUT') for c in in_cols]
flux[in_cols].plot.bar(stacked=True, ax=ax)
(-flux[out_cols]).plot.bar(stacked=True, ax=ax)
ax.legend(loc='lower left', bbox_to_anchor=(1, 0))
ax.axhline(0, lw=0.5, c='k')
ax.set_ylabel('Simulated Flux, in $m^3/d$')

[59]:

Text(0, 0.5, 'Simulated Flux, in $m^3/d$')
../../../_images/notebooks_part1_flopy_solutions_03_Loading_and_visualizing_models-solutions_107_1.png

Fienen, M. N., Haserodt, M. J., Leaf, A. T., and Westenbroek, S. M. (2022). Simulation of regional groundwater flow and groundwater/lake interactions in the central Sands, Wisconsin. U.S. Geological Survey Scientific Investigations Report 2022-5046. doi:10.3133/sir20225046

Fienen, M. N., Haserodt, M. J., and Leaf, A. T. (2021). MODFLOW models used to simulate groundwater flow in the Wisconsin Central Sands Study Area, 2012-2018. New York: U.S. Geological Survey Data Release. doi:10.5066/P9BVFSGJ

[ ]: